График восстановленной функциональной зависимости

по результатам измерений

называется кривой регрессии. Для проверки согласия построенной кривой регрессиис результатами эксперимента обычно вводят следующие числовые характеристики:коэффициент корреляции (линейная зависимость), корреляционное отношение икоэффициент детерминированности. При этом результаты обычно группируют ипредставляют в форме корреляционной таблицы. В каждой клетке этой таблицыприводятся численности

тех пар

, компонентыкоторых попадают в соответствующие интервалы группировки по каждой переменной.Предполагая длины интервалов группировки (по каждой переменной) равными междусобой, выбирают центры

(соответственно
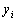
)этих интервалов и числа

в качестве основы для расчетов.Коэффициент корреляции является мерой линейной связи между зависимымислучайными величинами: он показывает, насколько хорошо в среднем может бытьпредставлена одна из величин в виде линейной функции от другой.Коэффициент корреляции вычисляется по формуле:

, (2.3.1)где

,

и

¾ среднее арифметическое значение соответственно по
x и
y. Коэффициент корреляции между случайными величинами по абсолютной величине непревосходит 1. Чем ближе

к 1, тем теснее линейная связь между
x и
y. В случае нелинейной корреляционной связи условные средние значениярасполагаются около кривой линии. В этом случае в качестве характеристикисилы связи рекомендуется использовать корреляционное отношение, интерпретациякоторого не зависит от вида исследуемой зависимости.Корреляционное отношение вычисляется по формуле:

, (2.3.2)где

, а числительхарактеризует рассеяние условных средних

около безусловного среднего

.Всегда
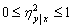
. Равенство
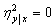
соответствует некоррелированным случайным величинам;

тогда и только тогда, когда имеется точная функциональная связь между
y и
x. В случае линейной зависимости
y от
x корреляционноеотношение совпадает с квадратом коэффициента корреляции. Величина

используется в качестве индикатора отклонения регрессии от линейной.Корреляционное отношение является мерой корреляционной связи
y с
x в какой угодно форме, но не может дать представления о степени приближенностиэмпирических данных к специальной форме. Чтобы выяснить насколько точнопостроенная кривая отражает эмпирические данные вводится еще однахарактеристика ¾ коэффициент детерминированности.Для его описания рассмотрим следующие величины.

- полная сумма квадратов, где

среднее значение
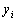
. Можно доказать следующее равенство

. Первое слагаемое равно

и называется остаточной суммой квадратов. Оно характеризует отклонениеэкспериментальных данных от теоретических.Второе слагаемое равно
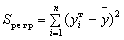
и называется регрессионной суммой квадратов и оно характеризует разброс данных.Очевидно, что справедливо следующее равенство

.Коэффициент детерминированности определяется по формуле:

. (2.3.3)Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тембольше значение коэффициента детерминированности

, который показывает, насколько хорошо уравнение, полученное с помощьюрегрессионного анализа, объясняет взаимосвязи между переменными. Если он равен1, то имеет место полная корреляция с моделью, т.е. нет различия междуфактическим и оценочным значениями y. В противоположном случае, есликоэффициент детерминированности равен 0, то уравнение регрессии неудачно дляпредсказания значений y.Коэффициент детерминированности всегда не превосходит корреляционное отношение.В случае когда выполняется равенство

то можно считать, что построенная эмпирическая формула наиболее точно отражаетэмпирические данные.
 по результатам измерений
по результатам измерений  называется кривой регрессии. Для проверки согласия построенной кривой регрессиис результатами эксперимента обычно вводят следующие числовые характеристики:коэффициент корреляции (линейная зависимость), корреляционное отношение икоэффициент детерминированности. При этом результаты обычно группируют ипредставляют в форме корреляционной таблицы. В каждой клетке этой таблицыприводятся численности
называется кривой регрессии. Для проверки согласия построенной кривой регрессиис результатами эксперимента обычно вводят следующие числовые характеристики:коэффициент корреляции (линейная зависимость), корреляционное отношение икоэффициент детерминированности. При этом результаты обычно группируют ипредставляют в форме корреляционной таблицы. В каждой клетке этой таблицыприводятся численности  тех пар
тех пар  , компонентыкоторых попадают в соответствующие интервалы группировки по каждой переменной.Предполагая длины интервалов группировки (по каждой переменной) равными междусобой, выбирают центры
, компонентыкоторых попадают в соответствующие интервалы группировки по каждой переменной.Предполагая длины интервалов группировки (по каждой переменной) равными междусобой, выбирают центры  (соответственно
(соответственно 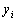 )этих интервалов и числа
)этих интервалов и числа  в качестве основы для расчетов.Коэффициент корреляции является мерой линейной связи между зависимымислучайными величинами: он показывает, насколько хорошо в среднем может бытьпредставлена одна из величин в виде линейной функции от другой.Коэффициент корреляции вычисляется по формуле:
в качестве основы для расчетов.Коэффициент корреляции является мерой линейной связи между зависимымислучайными величинами: он показывает, насколько хорошо в среднем может бытьпредставлена одна из величин в виде линейной функции от другой.Коэффициент корреляции вычисляется по формуле:  , (2.3.1)где
, (2.3.1)где  ,
,  и
и  ¾ среднее арифметическое значение соответственно по x и y. Коэффициент корреляции между случайными величинами по абсолютной величине непревосходит 1. Чем ближе
¾ среднее арифметическое значение соответственно по x и y. Коэффициент корреляции между случайными величинами по абсолютной величине непревосходит 1. Чем ближе  к 1, тем теснее линейная связь между x и y. В случае нелинейной корреляционной связи условные средние значениярасполагаются около кривой линии. В этом случае в качестве характеристикисилы связи рекомендуется использовать корреляционное отношение, интерпретациякоторого не зависит от вида исследуемой зависимости.Корреляционное отношение вычисляется по формуле:
к 1, тем теснее линейная связь между x и y. В случае нелинейной корреляционной связи условные средние значениярасполагаются около кривой линии. В этом случае в качестве характеристикисилы связи рекомендуется использовать корреляционное отношение, интерпретациякоторого не зависит от вида исследуемой зависимости.Корреляционное отношение вычисляется по формуле:  , (2.3.2)где
, (2.3.2)где  , а числительхарактеризует рассеяние условных средних
, а числительхарактеризует рассеяние условных средних  около безусловного среднего
около безусловного среднего  .Всегда
.Всегда 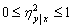 . Равенство
. Равенство 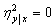 соответствует некоррелированным случайным величинам;
соответствует некоррелированным случайным величинам;  тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционноеотношение совпадает с квадратом коэффициента корреляции. Величина
тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционноеотношение совпадает с квадратом коэффициента корреляции. Величина  используется в качестве индикатора отклонения регрессии от линейной.Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенностиэмпирических данных к специальной форме. Чтобы выяснить насколько точнопостроенная кривая отражает эмпирические данные вводится еще однахарактеристика ¾ коэффициент детерминированности.Для его описания рассмотрим следующие величины.
используется в качестве индикатора отклонения регрессии от линейной.Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенностиэмпирических данных к специальной форме. Чтобы выяснить насколько точнопостроенная кривая отражает эмпирические данные вводится еще однахарактеристика ¾ коэффициент детерминированности.Для его описания рассмотрим следующие величины.  - полная сумма квадратов, где
- полная сумма квадратов, где  среднее значение
среднее значение 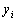 . Можно доказать следующее равенство
. Можно доказать следующее равенство  . Первое слагаемое равно
. Первое слагаемое равно  и называется остаточной суммой квадратов. Оно характеризует отклонениеэкспериментальных данных от теоретических.Второе слагаемое равно
и называется остаточной суммой квадратов. Оно характеризует отклонениеэкспериментальных данных от теоретических.Второе слагаемое равно 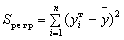 и называется регрессионной суммой квадратов и оно характеризует разброс данных.Очевидно, что справедливо следующее равенство
и называется регрессионной суммой квадратов и оно характеризует разброс данных.Очевидно, что справедливо следующее равенство  .Коэффициент детерминированности определяется по формуле:
.Коэффициент детерминированности определяется по формуле:  . (2.3.3)Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тембольше значение коэффициента детерминированности
. (2.3.3)Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тембольше значение коэффициента детерминированности  , который показывает, насколько хорошо уравнение, полученное с помощьюрегрессионного анализа, объясняет взаимосвязи между переменными. Если он равен1, то имеет место полная корреляция с моделью, т.е. нет различия междуфактическим и оценочным значениями y. В противоположном случае, есликоэффициент детерминированности равен 0, то уравнение регрессии неудачно дляпредсказания значений y.Коэффициент детерминированности всегда не превосходит корреляционное отношение.В случае когда выполняется равенство
, который показывает, насколько хорошо уравнение, полученное с помощьюрегрессионного анализа, объясняет взаимосвязи между переменными. Если он равен1, то имеет место полная корреляция с моделью, т.е. нет различия междуфактическим и оценочным значениями y. В противоположном случае, есликоэффициент детерминированности равен 0, то уравнение регрессии неудачно дляпредсказания значений y.Коэффициент детерминированности всегда не превосходит корреляционное отношение.В случае когда выполняется равенство  то можно считать, что построенная эмпирическая формула наиболее точно отражаетэмпирические данные.
то можно считать, что построенная эмпирическая формула наиболее точно отражаетэмпирические данные.





