Постановка задачи.
1. Используя метод наименьших квадратов функцию
, заданную таблично, аппроксимироватьа) многочленом первой степени 
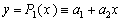;б) многочленом второй степени 
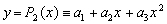;в) экспоненциальной зависимостью 
.2. Для каждой зависимости вычислить коэффициент детерминированности.3. Вычислить коэффициент корреляции (только в случае а).4. Для каждой зависимости построить линию тренда.5. Используя функцию ЛИНЕЙН вычислить числовые характеристикизависимости y от x. 6. Сравнить свои вычисления с результатами, полученными при помощи функцииЛИНЕЙН.7. Сделать вывод, какая из полученных формул наилучшим образом аппроксимируетфункцию .8. Написать программу на одном из языков программирования и сравнитьрезультаты счета с полученными выше.
Расчетные формулы.
2.1 Построение эмпирических формул методом наименьших квадратов Очень часто, особенно при анализе эмпирических данных возникает необходимостьнайти в явном виде функциональную зависимость между величинами x и y, которые получены в результате измерений.При аналитическом исследовании взаимосвязи между двумя величинами x и yпроизводят ряд наблюдений и в результате получается таблица значений:| x | 
| 
| ¼ | 
| ¼ | 
|
| y | 
| 
| ¼ | 
| ¼ | 
|
(независимая величина) задается экспериментатором, а получается в результате опыта. Поэтому эти значения будем называть эмпирическими или опытными значениями.Между величинами x и y существует функциональная зависимость, но ееаналитический вид обычно неизвестен, поэтому возникает практически важнаязадача - найти эмпирическую формулу 
(2.1.1)(где 
- параметры),значения которой при 
возможно мало отличались бы от опытных значений 
.Обычно указывают класс функций (например, множество линейных, степенных,показательных и т.п.) из которого выбирается функция 
, и далее определяются наилучшие значения параметров.Если в эмпирическую формулу (2.1.1) подставить исходные , то получим теоретические значения 
, где 
.Разности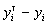 
называютсяотклонениями и представляют собой расстояния по вертикали от точек 
до графика эмпирической функции.Согласно методу наименьших квадратов наилучшими коэффициентами считаются те, для которых сумма квадратов отклонений найденной эмпирическойфункции от заданных значений функции 
(2.1.2)будет минимальной.Поясним геометрический смысл метода наименьших квадралтов.Каждая пара чисел 
из исходной таблицы определяет точку на плоскости 
. Используя формулу (2.1.1) при различных значениях коэффициентов можно построить ряд кривых, которые являются графиками функции (2.1.1). Задачасостоит в определении коэффициентов таким образом, чтобы сумма квадратов расстояний по вертикали от точек 
до графика функции (2.1.1) была наименьшей.Построение эмпирической формулы состоит из двух этапов: выяснение общего видаэтой формулы и определение ее наилучших параметров.Если неизвестен характер зависимости между данными величинами x и y, то вид эмпирической зависимости является произвольным. Предпочтение отдаетсяпростым формулам, обладающим хорошей точностью. Удачный выбор эмпирическойформулы в значительной мере зависит от знаний исследователя в предметнойобласти, используя которые он может указать класс функций из теоретическихсоображений. Большое значение имеет изображение полученных данных в декартовыхили в специальных системах координат (полулогарифмической, логарифмической ит.д.). По положению точек можно примерно угадать общий вид зависимости путемустановления сходства между построенным графиком и образцами известных кривых.Определение наилучших коэффициентов входящих в эмпирическую формулу производят хорошо известными аналитическимиметодами.Для того, чтобы найти набор коэффициентов , которые доставляют минимум функции S, определяемой формулой (2.1.2),используем необходимое условие экстремума функции нескольких переменных -равенство нулю частных производных. В результате получим нормальную системудля определения коэффициентов 
: 
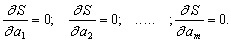(2.1.3)Таким образом, нахождение коэффициентов 
сводится к решению системы (2.1.3).Эта система упрощается, если эмпирическая формула (2.1.1) линейна относительнопараметров , тогдасистема (2.1.3) - будет линейной.Конкретный вид системы (2.1.3) зависит от того, из какого класса эмпирическихформул мы ищем зависимость (2.1.1). В случае линейной зависимости 
система (2.1.3) примет вид: 
(2.1.4)Эта линейная система может быть решена любым известным методом (методомГаусса, простых итераций, формулами Крамера).В случае квадратичной зависимости 
система (2.1.3) примет вид: 
(2.1.5)
