| Вариант 1 | Вариант 2 |

|

|
| Вариант 3 | Вариант 4 |

|

|
| Вариант 5 | Вариант 6 |

|

|
| Вариант 7 | Вариант 8 |

|

|
| Вариант 9 | Вариант 10 |

|

|
| Вариант 11 | Вариант 12 |

|

|
| Вариант 13 | Вариант 14 |

|

|
| Вариант 15 | Вариант 16 |

|

|
Приложение Б
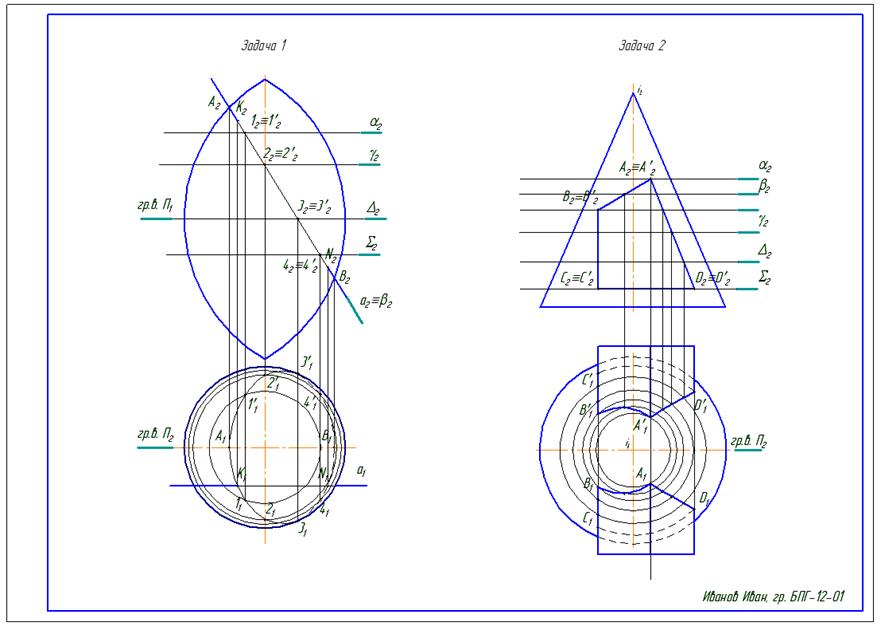
Рисунок 5 – Образец выполнения КГР: задачи №1 и №2.

Рисунок 6 – Образец выполнения КГР: задачи №3 и №4.
Контрольные вопросы
1. Алгоритм решения задачи на построение линии пересечения многогранников.
2. Алгоритм решения задачи на построение линии пересечения кривой поверхности плоскостью.
3. В чем заключается общий прием построения точек пересечения прямой с кривой поверхностью способом вспомогательных секущих плоскостей. Применение способа.
4. В каких случаях применяется способ вспомогательных секущих плоскостей при построении линии пересечения поверхностей.
5. Какие поверхности называются соосными.
6. Какие условия введения вспомогательных секущих концентрических сфер должны выполняться при построении линии пересечения кривых поверхностей.
7. Определение максимальной и минимальной вспомогательных концентрических сфер.
8. Какие точки называются характерными (опорными) при построении линии пересечения двух поверхностей.
9. Какие точки называются точками видимости.
10. Что называется разверткой поверхности.
11. Какие поверхности относятся к развертываемым и условно развертываемым.
12. В каких случаях при построении развертки применяется способ «нормального сечения». Суть способа.
13. В каких случаях при построении развертки применяется способ «раскатки». Суть способа.






