Развертываемые Неразвертываемые
Много- Кони- Цилинд- Торсо- Вин- Пов- Враще- Парал. Каркас-
гранни- ческие рические вые и то- ти ния пере- ные
ки с реб- вые Ката- носа (сетки)
ром лана
возвра-
та
В основу классификации поверхностей закладывают или вид образующей, или закон ее движения.
В зависимости от формы образующей поверхности делятся на линейчатые, когда образующей служит прямая, и нелинейчатые, когда образующей служит кривая линия.
По закону движения образующих имеются поверхности с вращательным движением – поверхности вращения; с поступательным движением – поверхности параллельного переноса; с винтовым движением – винтовые поверхности.
По признаку развертывания – развертываемые и неразвертываемые.
Развертываемой называется поверхность, которую можно развернуть до совмещения с плоскостью без складок и разрывов.
Неразвертываемой называется поверхность, которую можно развернуть только условно.
Для изображения поверхности на чертеже выделяют некоторое количество линий, которые образуют линейный каркас поверхности.
Если закон движения образующей и ее форма заданы определенным образом, то поверхность в начертательной геометрии определяют образующей и условием ее перемещения. Чтобы указать, какая именно поверхность изображена на чертеже необходимо знать, что является определителем каждой поверхности. При этом чертеж поверхности должен быть таким, чтобы на нем можно было выделить и построить любую линию и точку, принадлежащие поверхности.
Совокупность геометрических элементов и условий, необходимых и достаточных для однозначного задания поверхности в пространстве и на чертеже, называют определителем кинематическойповерхности.
Определитель поверхности содержит две части – геометрическую и алгоритмическую. Геометрическая – это вид образующей и направляющих; алгоритмическая - закон движения образующей.
Поверхность считается заданной, если относительно любой точки пространства однозначно решается вопрос о принадлежности ее к данной поверхности.
Точка принадлежит поверхности, если она лежит на линии, принадлежащей этой поверхности.
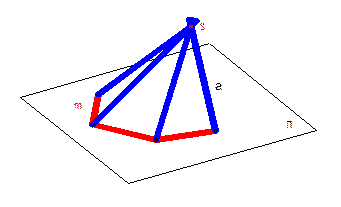
Гранные поверхности образуются перемещением прямолинейной образующей по ломаной направляющей.
При этом, если одна точка (S) образующей неподвижна, создается пирамидальная поверхность. Если образующая при перемещении параллельна заданному направлению (S), то создается призматическая поверхность. Определителем пирамидальной поверхности являются ломаная направляющая и точка, через которую проходят все образующие. А определителем призматической поверхности являются ломаная направляющая и прямая образующая, параллельно которой проводятся все ребра поверхности.
Элементы гранных поверхностей: грани, ребра, основание, вершина.
 | |||||
 | |||||
 | |||||
Часть пространства, ограниченная со всех сторон поверхностью, называют геометрическим телом.
Многогранником называют тело, ограниченное плоскими многоугольниками.
Совокупность всех ребер и вершин многогранника называется его сеткой. Сетка полностью задает многогранник и может служить его определителем. (т.е. по изображению мы можем определить, какой именно многогранник задан).
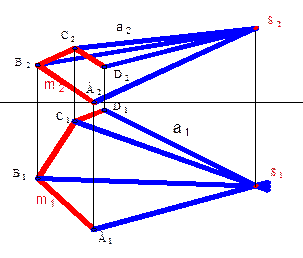
Коническая поверхность образуется перемещением прямолинейной образующей l по криволинейной направляющей. При этом все образующие проходят через вершину S. Определителем конической поверхности являются криволинейная направляющая и вершина S.
 | |||
 | |||
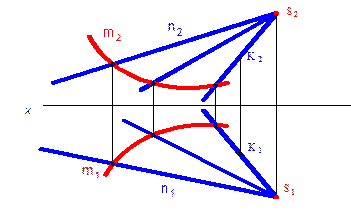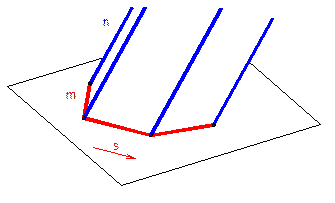
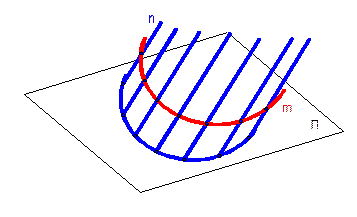
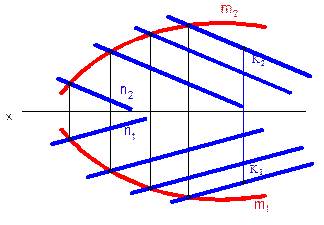
Цилиндрическая поверхность образуется движением прямой l по криволинейной направляющей m параллельно заданному направлению t.
Цилиндрическую поверхность можно рассматривать как частный случай конической поверхности с бесконечно удаленной вершиной S. Определителем цилиндрической поверхности являются криволинейная направляющая и направление t.
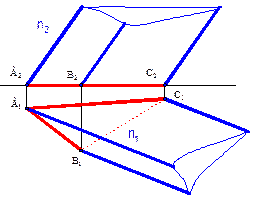
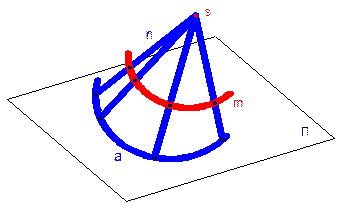
Торсом называется поверхность, образованная прямолинейной образующей l, касающейся при своем движении во всех своих положениях некоторой пространственной кривой m, называемой ребром возврата.
 |
Коническая и цилиндрическая поверхности являются частными случаями торса.
Винтовой называется поверхность, образованная винтовым движением образующей l вокруг оси i.
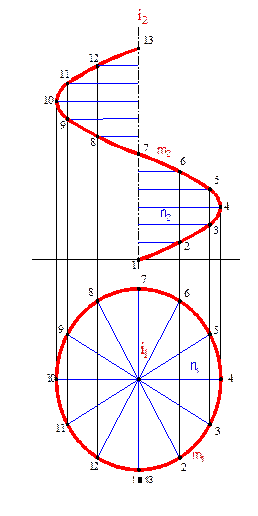Определитель винтовой поверхности Ф состоит из оси i, направляющей винтовой линии q и образующей l. Ф (i,q, l)
