Термин корреляции (лат. correlatio —соотношение, связь) впервые применил Ж. Кювье в труде «Лекции по сравнительной анатомии» (1806г.). А самый метод корреляции вошел в науку из практических задач морфологии и генетики. Математические обоснования метода даны Огюстом Браве в 1846 году. Однако Браве (1811—1863) имел в виду «теорию ошибок в плоскости», т. е. распространение закона ошибок Гаусса на случаи двух переменных Y и X, и биологическими корреляциями не занимался.
Первыми, кто использовал и развил метод корреляции, были Гальтон и Пирсон, занимавшиеся изучением проблемы наследственности и изменчивости. С именем Гальтона связано и введение термина корреляция в биометрию (1886г.).
Кроме функциональной связи между переменными 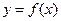 , существует вероятностная (стохастическая) связь между случайными величинами x и у. Эта связь проявляется в изменении закона распределения у при изменении распределения х. Так, вероятностная связь между случайными медико-биологическими параметрами организма обнаруживается всегда, когда одни и те же случайные факторы (внешние условия, внутренние патологические изменения, раздражители и т. д.) влияют на эти исследуемые параметры.
, существует вероятностная (стохастическая) связь между случайными величинами x и у. Эта связь проявляется в изменении закона распределения у при изменении распределения х. Так, вероятностная связь между случайными медико-биологическими параметрами организма обнаруживается всегда, когда одни и те же случайные факторы (внешние условия, внутренние патологические изменения, раздражители и т. д.) влияют на эти исследуемые параметры.
Выявление связей (корреляций) между различными случайными переменными и случайными процессами широко используется в медицинской диагностике. С помощью корреляционного анализа решаются задачи установления обоснованного диагноза. Целью диагноза является установление с высокой надежностью заболевания при определенных значениях признаков (симптомов). Поэтому установление корреляций между различными показателями состояния больного и влияние их изменений на жизнедеятельность организма является важной задачей лабораторных и клинических исследований.
Более того; все системы, органы, ткани, клетки целостного организма находятся в корреляционной связи друг с другом. Благодаря различным формам корреляций (химических, нервных, морфофизиологических, эволюционных и др.) организм проявляется как единая сложная целостная система.
Теория метода.
Пусть в результате эксперимента получены случайные значения одновременно измеряемых величин X и Y. Выборка  состоит из значений х1; х2;, х3;...хп, а выборка
состоит из значений х1; х2;, х3;...хп, а выборка  из значений y1, у2, у3,...уn. Если попарно нанести на плоскость точки, соответствующие (х) и (у) в первой, второй, п - й реализации, то они займут определенную область, называемую корреляционным полем.
из значений y1, у2, у3,...уn. Если попарно нанести на плоскость точки, соответствующие (х) и (у) в первой, второй, п - й реализации, то они займут определенную область, называемую корреляционным полем.
Как правило, если между случайными величинами (x) и (у) существует связь, то корреляционное поле имеет вид эллипса со сгущением точек вокруг главной оси и с малым числом их на периферии (рис. 1).
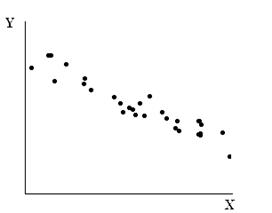

Рис.1 Рис.2
Если связь выражена слабо, то разброс точек велик (рис. 2). Величину связи можно
оценить, задав уравнение линии регрессии. Эта линия проходит наиболее близко ко всем точкам корреляционного поля.
При корреляциях между X и Y мерой рассеяния могут служить выборочные стандартные отклонения.

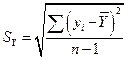
Простейшей характеристикой связи между случайными величинами (х) и (у) служит коэффициент ковариации  , который может быть вычислен для выборки из n реализаций, как
, который может быть вычислен для выборки из n реализаций, как

Коэффициентом корреляции называется безразмерная величина

Или

Коэффициент корреляции R количественно характеризует связь между случайными величинами или процессами. Он изменяется от +1 до -1. Отрицательные значения указывают на обратную зависимость между величинами (x) и (у) (возрастание одной при убывании другой). Прямая связь между величинами существует при положительных значениях коэффициента корреляции R. Корреляция будет полной при R = + 1 и отсутствует при R = 0. Практически считается, что при | R | < 0,4 связь отсутствует, при 0,4 <│ R │ < 0,7 имеется слабая связь. Тесная взаимосвязь между случайными величинами или процессами (х) и (у) имеется при 0,7 < │ R |<1.
В качестве критерия близости точек корреляционного поля к линии регрессии может также приниматься минимум суммы квадратов отклонений точек от этой линии, заданной в виде уравнения:
у = ах + b
(см. Метод наименьших квадратов)
Статистическая теория случайных величин и процессов позволяет определить коэффициент „ а " и „ в " через 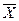 ,
, 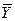 ,
,  ,
, 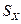 и коэффициент корреляции R:
и коэффициент корреляции R:

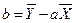
Вычислив (a) и (b), можно по уравнению у = ах + b получить прямую регрессии.
Выборочный коэффициент корреляции, являясь величиной случайной, подчиняется закону нормального распределения Гаусса. Для малых выборок (n < 100) используют распределение Стьюдента, его критерий  определяют по формуле
определяют по формуле

Он позволяет вычислить степень достоверности результата. Обычно результат оценивается как достоверный, если вероятность ошибки менее 5% (P оши6ки<0,05). Вычислив t и зная п, по таблице Стьюдента можноопределить Ротибки.
Пример 8
Полоскание с хлоргексидином предотвращает образование зубного налета. Ф. Эшли и соавторы сравнили эффективность полоскания. Участники исследования полоскали рот, после чего зубной налет отделяли и взвешивали. Налет оценивали так же визуально по специально разработанной шкале. Чтобы оценить точность визуальных оценок, их сравнивали с результатами взвешивания. Результаты представлены в табл.
| № | ||||||||||
| Сухой вес зубного налета, мГ | 2,7 | 1,2 | 2,7 | 2,1 | 3,5 | 2,8 | 3,7 | 8,9 | 5,8 | 4,0 |
| Визуальная оценка зубного налета, баллы |
Требуется оценить степень корреляционной связи между исследованными параметрами и достоверность этой связи.
Для наглядности, нанесем экспериментальные данные в виде точек на график.

Для расчета коэффициента корреляции заполним табл.
| № | 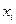
| 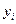
| 
| 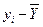
| 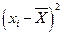
| 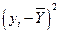
| 
|
| 2.7 | -34.60 | -1.04 | 1.20e3 | 1.08 | 35,98 | ||
| 1.2 | -27.60 | -2.54 | 761.76 | 6.45 | 70,10 | ||
| 2.7 | -14.60 | -1.04 | 213.16 | 1.08 | 15,18 | ||
| 2.1 | 0.40 | -1.64 | 0.16 | 2.69 | - 0,66 | ||
| 3.5 | 0.40 | -0.24 | 0.16 | 0.06 | - 0,10 | ||
| 2.8 | 5.40 | -0.94 | 29.16 | 0.88 | - 5,08 | ||
| 3.7 | 8.40 | -0.04 | 70.56 | 0.00 | - 0,34 | ||
| 8.9 | 18.40 | 5.16 | 338.56 | 26.63 | 94,94 | ||
| 5.8 | 20.40 | 2.06 | 416.16 | 4.24 | 42,02 | ||
| 4.0 | 23.40 | 0.26 | 547.56 | 0.07 | 6,08 | ||
| Сумма Σ | 37,4 | 3577,24 | 43,18 | 258,12 | |||
| Среднее значение | 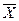 =59,6 =59,6
| 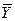 =3,74 =3,74
| ----- | ------ | ---------- | ---------- | --------------------- |

Имеется тесная связь между исследованными параметрами. Оценим достоверность этой связи. Для этого определим коэффициент Стьюдента.

По таблице (см. приложение 2) по рассчитанному коэффициенту Стьюдента определяем доверительную вероятность Р = 0, 96. Т.е с вероятность Р = 0, 96 между исследованными параметрами существует тесная (R = 0,7) прямая (0 < R) корреляционная связь. Обработав экспериментальные данные методом наименьших квадратов, получим прямую регрессии.


Эта линия является наилучшим усреднением экспериментальных точек.
Приложение 1
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ НА ОСНОВЕ ЗАКОНА ГУАССА
Точечные оценки математического ожидания и дисперсии.
Пусть истинное значение измеряемой величины - X, а x1,х2,..., хn - ряд её отсчетов. Пусть наблюдаемые значения имеют нормальное распределение с математическим ожиданием µ, совпадающим с истинным значением, и некоторой дисперсией σ 2. Вероятность того, что все отсчеты попадут в бесконечно малый интервал
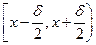 по теореме умножения вероятностей равна произведению вероятностей того, что каждый отсчет попадет в этот интервал
по теореме умножения вероятностей равна произведению вероятностей того, что каждый отсчет попадет в этот интервал

Чем больше Р, тем с большей вероятность наблюдаемые значения группируются вокруг истинного значения. Функция  с аргументами
с аргументами  называется правдоподобием эксперимента.
называется правдоподобием эксперимента.
Найдем, при какой связи 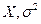 с отсчетами x1, х2,….., xn правдоподобие максимально. При исследовании функции на экстремум удобно использовать не саму функцию, а ее логарифм.
с отсчетами x1, х2,….., xn правдоподобие максимально. При исследовании функции на экстремум удобно использовать не саму функцию, а ее логарифм.
 .При фиксированном значении
.При фиксированном значении  максимум L достигается при
максимум L достигается при 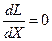 т.е.
т.е. 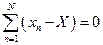
Из последнего уравнения находим:
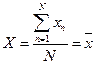
Следовательно, выборочное среднее значение есть максимально правдоподобная оценка истинного значения измеряемой величины.
При фиксированном аргументе 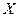 значение
значение  , дающее максимум
, дающее максимум  , можно найти из уравнения:
, можно найти из уравнения:
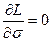 или
или 
Тогда 
Следовательно, максимально правдоподобная оценка стандартного квадратического отклонения равна выборочному среднему квадратическому отклонению отсчетов от истинного значения.
Так как в процессе измерений истинное значение неизвестно, то полученная формула не пригодна для расчета погрешности. Выразим  через
через 

В этом выражении второе слагаемое равно нулю. Рассмотрим третье слагаемое.

Второе слагаемое полученного выражения равно нулю при  , т.к. отклонение наблюдаемых значений от истинного встречаются с разными значениями одинаково часто. Следовательно
, т.к. отклонение наблюдаемых значений от истинного встречаются с разными значениями одинаково часто. Следовательно

Величина 
называется выборочным средним квадратическим отклонением одиночного наблюдения, котороев пределе дает максимально правдоподобнуюоценку стандартного квадратического отклонения:

При конечном значении 
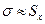
Выборочное среднее является суммой N нормально распределенных случайных величин, имеющих одинаковую дисперсию. Оно представляет случайную величину с дисперсией в N раз меньшей, чем дисперсия слагаемых. Поэтому выборочное среднее квадратическое отклонение среднего 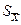 в
в  раз меньше чем
раз меньше чем 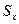 т.е.
т.е.

Приложение 2
Таблица параметров распределения Стъюдента
при 8 степенях свободы (m = 8)
t - коэффициент Стъюдента Р - вероятность
| t | Р | t | Р | t | Р | t | Р | t | Р |
| 3.355 | 0.99 | 1.508 | 0.83 | 1.037 | 0.67 | 0.723 | 0.51 | 0.471 | 0.35 |
| 2.896 | 0.98 | 1.469 | 0.82 | 1.015 | 0.66 | 0.706 | 0.50 | 0.457 | 0.34 |
| 2.634 | 0.97 | 1.432 | 0.81 | 0.993 | 0.65 | 0.690 | 0.49 | 0.442 | 0.33 |
| 2.449 | 0.96 | 1.397 | 0.80 | 0.971 | 0.64 | 0.673 | 0.48 | 0.428 | 0.32 |
| 2.306 | 0.95 | 1.363 | 0.79 | 0.950 | 0.63 | 0.656 | 0.47 | 0.414 | 0.31 |
| 2.189 | 0.94 | 1.331 | 0.78 | 0.929 | 0.62 | 0.640 | 0.46 | 0.399 | 0.30 |
| 2.090 | 0.93 | 1.299 | 0.77 | 0.909 | 0.61 | 0.624 | 0.45 | 0.385 | 0.29 |
| 2.004 | 0.92 | 1.269 | 0.76 | 0.889 | 0.60 | 0.608 | 0.44 | 0.371 | 0.28 |
| 1.928 | 0.91 | 1.240 | 0.75 | 0.869 | 0.59 | 0.592 | 0.43 | 0.357 | 0.27 |
| 1.860 | 0.90 | 1.212 | 0.74 | 0.850 | 0.58 | 0.577 | 0.42 | 0.344 | 0.26 |
| 1.797 | 0.89 | 1.185 | 0.73 | 0.831 | 0.57 | 0.561 | 0.41 | 0.330 | 0.25 |
| 1.740 | 0.88 | 1.159 | 0.72 | 0.813 | 0.56 | 0.546 | 0.40 | 0.316 | 0.24 |
| 1.687 | 0.87 | 1.133 | 0.71 | 0.794 | 0.55 | 0.531 | 0.39 | 0.302 | 0.23 |
| 1.638 | 0.86 | 1.108 | 0.70 | 0.776 | 0.54 | 0.516 | 0.38 | 0.289 | 0.22 |
| 1.592 | 0.85 | 1.084 | 0.69 | 0.758 | 0.53 | 0.501 | 0.37 | 0.275 | 0.21 |
| 1.549 | 0.84 | 1.060 | 0.68 | 0.741 | 0.52 | 0.486 | 0.36 | 0.262 | 0.20 |
Коэффициенты Стьюдента при различных степенях свободы (m)
| Вероятность Р | ||||||
| № | 0,5 | 0,9 | 0,95 | 0,98 | 0,99 | 0,999 |
| 6,3 | 12,7 | 31,8 | 63,7 | 636,6 | ||
| 0,82 | 2,9 | 4,32 | 7,0 | 9,9 | 31,6 | |
| 0,77 | 2,4 | 3,21 | 4,5 | 5,8 | 12,9 | |
| 0,74 | 2,1 | 2,78 | 3,7 | 4,6 | 8,6 | |
| 0,73 | 2,0 | 2,61 | 3,4 | 4,0 | 6,9 | |
| 0,72 | 1,9 | 2,42 | 3,1 | 3,7 | 6,0 | |
| 0,71 | 1,9 | 2,42 | 3,0 | 3,5 | 5,4 | |
| 0,71 | 1,9 | 2,31 | 2,9 | 3,4 | 5,0 | |
| 0,70 | 1,8 | 2,30 | 2,8 | 3,2 | 4,8 | |
| 0,69 | 1,7 | 2,11 | 2,5 | 2,8 | 3,8 | |
| 0,67 | 1,6 | 2,02 | 2,5 | 2,8 | 3,3 |
Литература
1.Камке Д., Кремер К., Физические основы единиц измерения. М., Мир, 1980
2.Чертов А.Г., Физические величины. М., Высшая школа, 1990
3.Международный стандарт ИСО 31/0
4.Зайдель А.Н., Ошибки измерений физических величин, М., Наука 1974
5.Тейлор Д., Введение в теорию ошибок, М., Мир, 1985
6.Лакин Г.Ф., Биометрия. М., Высшая школа,1990
7.Гланц Г, Медико-биологическая статистика, М.Практика, 1999
Содержание Стр.
1. Погрешности измерений……………………………………..4 - 15
2. Графическое представление результатов измерений……...15 - 20.
3. Метод наименьших квадратов……………………………...20 - 24
4. Корреляционный анализ …………………………………....25 - 29
5. Приложение………………………………………………….30 - 31
6. Литература…………………………………………………..32






