Высшего профессионального образования
«Московский государственный медико-
стоматологический университет»
Федерального агентства по здравоохранению
И социальному обеспечению
КАФЕДРА МЕДИЦИНСКОЙ И БИОЛОГИЧЕСКОЙ ФИЗИКИ
В.С. Воеводский, В.М.Говорун
Математическая обработка результатов измерений.
Учебное пособие для студентов стоматологического факультета
Москва, 2009
Государственное образовательное учреждение
Высшего профессионального образования
«Московский государственный медико-
стоматологический университет»
Федерального агентства по здравоохранению
И социальному обеспечению
КАФЕДРА МЕДИЦИНСКОЙ И БИОЛОГИЧЕСКОЙ ФИЗИКИ
В.С. Воеводский, В.М.Говорун
Математическая обработка результатов измерений.
Учебное пособие для студентов стоматологического факультета
Москва, 2009
ББК 22.3 я 73
С88
УДК 53 (075.8)
Рецензенты:
А.С.Берлянд - профессор зав. кафедры общей и биоорганической химии
МГМСУ доктор фарм. наук.
С.А.Вознесенский - доцент кафедры медицинской и биологической физики
ММА им. И.М.Сеченова, кандидат физ. - мат. наук.
С88 В.С.Воеводский, В.М.Говорун.
Математическая обработка результатов измерений.
Учебное пособие.
М.: МГМСУ, 2009, 30c.
В представленном методическом пособии рассмотрены вопросы обработки экспериментальных данных, с которыми сталкиваются студенты при проведении лабораторных и практических занятий. В частности рассмотрены вопросы возникновения приборных, случайных и грубых погрешностей. На конкретных примерах приводятся методы оценки этих погрешностей.
Рассмотрены вопросы, возникающие при прямых и косвенных измерениях.
Значительная часть пособия посвящена графическим методам представления данных. На примерах из медицинской практики проиллюстрированы, как метод наименьших квадратов, применяемый для обработки экспериментальных данных, так и основы корреляционного анализа.
Издается по решению Ученого совета МГМСУ
(Протокол №8 от 27 мая 2008г.)
ББК 22.3 я 73
© МГМСУ, 2009
© Кафедра медицинской и биологической физики МГМСУ, 2009
© Владимир Сергеевич Воеводский,
Вадим Маркович Говорун. 2009
I.Погрешности измерений
В повседневной жизни мы непрерывно сталкиваемся с необходимостью, что - то измерить.
Измерить - значит сравнить интересующую нас величину с эталоном этой величины. Исторически были установлены некоторые эталоны, например, метр, килограмм, секунда. Из установленных эталонов образуются системы единиц. В используемой в настоящее время системе единиц СИ такими эталонами являются метр, секунда, килограмм, градус Кельвина, сила тока ампер, сила света кандела, единица количества вещества моль и единицы измерения углов радиан и стерадиан.
Следовательно, если мы, например, измеряем линейные размеры тела, то мы тем самым устанавливаем, сколько кратных долей эталона длины метра содержится в интересующем нас теле. То же самое относится и к измерению массы, времени, других величин.
Но любые измерения всегда связаны с некоторыми ошибками или погрешностями.
Справедлива поговорка: “Не ошибается только тот, кто ничего не делает». Следовательно, «абсолютно точно» ничего измерить в принципе невозможно. Отсюда возникают две основные задачи:
а) измерять как можно точнее,
б) уметь оценить погрешность, которую мы при измерениях неизбежно совершаем.
Говорят о погрешностях прямых и косвенных измерений. Строго говоря, косвенных измерений не существует. Имеется в виду, что интересующая нас величина не измеряется напрямую, а рассчитывается по соответствующим математическим формулам. Например, при определении объема шара напрямую измеряется его диаметр, а объем рассчитывается по известной формуле. Тем самым, объем шара определяется с некоторой погрешностью, которую и называют погрешностью косвенного измерения.
Неизбежно совершаемые при измерениях ошибки или погрешности принято разделять на систематические, приборные и случайные.
Систематические погрешности чаще всего связывают c техническим несовершенством самого измерительного устройства. Например, «портняжный сантиметр» может в течение длительной эксплуатации немного вытянуться. При этом в дальнейшем при его использовании будет совершаться систематическая ошибка, приводящая к уменьшению реальных размеров измеряемых тел. Часы, постоянно спешащие или отстающие, так же приводят к систематическим погрешностям. Систематические погрешности не столь принципиальны, так как могут быть всегда учтены. Зная, что часы спешат или отстают можно всегда скорректировать время.
1. С приборными погрешностями дело обстоит сложнее. Эти погрешности присуще самому измерительному устройству (качеству его изготовления или заложенному в нем принципу измерения). Аналоговые приборы характеризуются ценой деления, а цифровые разрядность отображаемых на экранах величин. Цена деления – это наименьшая величина, которая может быть измерена данным прибором. Строго говоря, «на глаз», можно всегда установить ближе к какому делению, например, расположена стрелка измерительного прибора. Поэтому принято считать, что приборная погрешность равна половине цены деления измерительного устройства. Рис.1
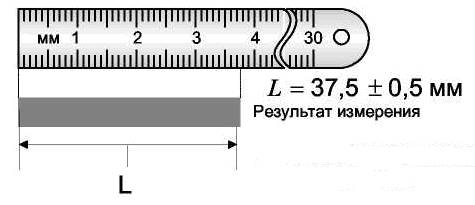
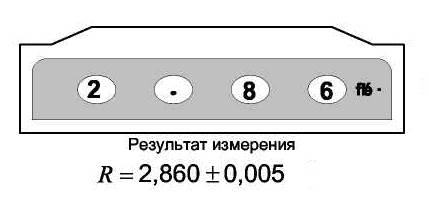
Аналоговые измерительные устройства характеризуются классом точности, который указывается на их шкале. Класс точности выражается в процентах и дает возможность рассчитать погрешность прибора. Для этого надо предельную величину, измеряемую данным прибором умножить на его класс точности. Единица деления шкалы наносится исходя из этих соображений. Следует иметь в виду, что для обеспечения большей точности измерений, надо стремиться работать на приборе так, чтобы отклонении стрелки было наибольшим. Необходимо помнить, что приборные погрешности определяют максимальную точность измерений. Измерить точнее, чем точность измерительного прибора невозможно.
2. Случайные погрешности уже по своему названию подчеркивают случайность получаемых результатов. Эти погрешности носят вероятностный характер. Они поддаются математической обработке, в основе которой лежит теория вероятности.
Основная особенность случайных погрешностей (в отличие от систематических) заключается в том, что они встречаются как в сторону занижения, так и завышения результатов измерений, причем примерно с равной вероятностью. Вторая отличительная их особенность заключается в том, что чем больше погрешность, тем меньше ее вероятность. Более вероятно, что мы меньше ошибаемся.
Пример 1
Было проведено 25 измерений некоторой величины. Результаты представлены на рис.2
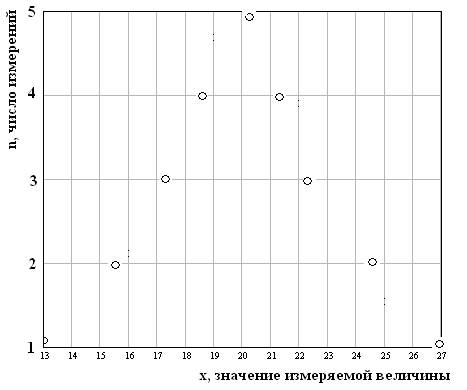
Рис.2
Из рисунка видно, что, например, значение Х = 20 было получено при 5 измерениях, значения Х = 13 и Х = 27, значительно отличающиеся от Х = 20, были получены только в одном измерении.
Случайные погрешности подчиняются закону нормального распределения, или закону Гаусса.
Иногда говорят еще о грубых ошибках или промахах («полученный результат не лезет ни в какие ворота»). О выявлении их мы поговорим позже.
И так, подытожим:
1.Для борьбы с систематическими погрешностями надо измерительное устройство либо
отремонтировать, либо заменить.
2.Для борьбы с приборными погрешностями надо взять более точные приборы (повысить
класс точности прибора).
3.Для борьбы со случайными и грубыми погрешностями надо научиться их математически
обрабатывать.
Предположим, что устранены систематические и грубые погрешности, тогда общая погрешность складывается из приборной и случайной. Очевидно, что результат будет зависеть от их соотношения. Если приборная погрешность на много больше случайной, то случайной погрешностью можно пренебречь и наоборот. На практике под «на много больше» имеется в виду в 5 раз. Если это соотношение меньше, то необходимо учитывать и ту и другую погрешности.
Пример 2.
При 5 измерениях диаметра шарика штангенциркулем (рис.3)
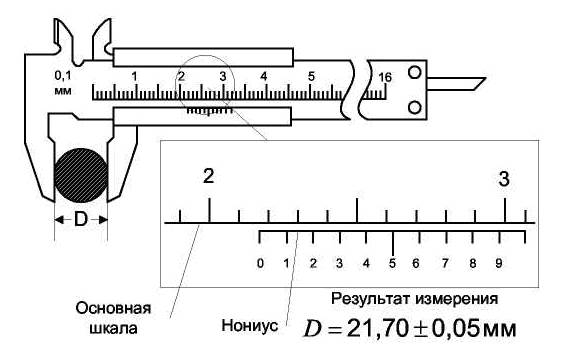
Рис.3
были получены одинаковые значения диаметра D = 21,70мм. Так как получены одинаковые значения, говорить о случайной погрешности бессмысленно. Общая погрешность будет равна приборной и в нашем случае, учитывая, что цена деления штангенциркуля равна 0,1мм, приборная погрешность будет равна 0,05мм (половине цены деления).
Таким образом, если в серии измерений получается одинаковый результат, то общая погрешность измерений равна половине цены деления измерительного инструмента.
Если в серии измерений получаются различные результаты, то необходимо оценить случайную погрешность и сопоставить ее с приборной.
3.Оценка случайной погрешности.
Пусть в серии измерений получен ряд значений измеряемой величины. Измеряемую величину будем обозначать Х, а ее численные значения {x1, x2, x3, …..x n}. Будем это называть выборкой.
Наиболее близким к истинному (никогда неизвестному) значению является среднее выборочное значение. (см. приложение 1)
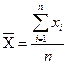 (1)
(1)
Но эта величина не определяет разброс случайной величины около среднего значения. Для характеристики разброса вводятся, так называемые, остаточные разности, характеризующие отклонение результата отдельных измерений 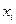 от среднего выборочного значения
от среднего выборочного значения 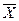
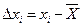
В среднем величину этого разброса 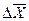 можно было бы определить как среднее значение остаточных разностей.
можно было бы определить как среднее значение остаточных разностей.
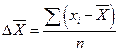 (2)
(2)
Однако, как не трудно показать, эта величина равна нулю и не может характеризовать разброс.
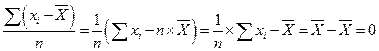 (3)
(3)
Полученное равенство полезно использовать для проверки вычисления среднего значения. Если при его вычислении не допущено арифметических ошибок, то сумма остаточных разностей должна быть равна нулю или, с учетом округления, незначительно отличаться от него.
Чтобы избежать нулевого результата, остаточные разности возводятся в квадрат и усредняются.
Полученная при этом величина носит название выборочной дисперсии.
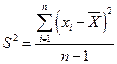 (4)
(4)
Размерность дисперсии равна квадрату размерности измеряемой величины. Это не дает возможности ни складывать, ни вычитать ее из измеряемой величины. Поэтому, извлекая из нее квадратный корень, вводят выборочное стандартное отклонение.
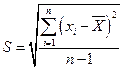 (5)
(5)
Появление в знаменателях у последних формул 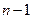 вместо
вместо 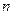 строго доказывается в теории ошибок (см. приложение1). Однако обосновать это можно следующим образом. Предположим, что мы сделали только одно измерение. Понятно, что при этом ничего нельзя сказать о разбросе. Это же следует и из выражения (5). Действительно, подставляя в это выражение
строго доказывается в теории ошибок (см. приложение1). Однако обосновать это можно следующим образом. Предположим, что мы сделали только одно измерение. Понятно, что при этом ничего нельзя сказать о разбросе. Это же следует и из выражения (5). Действительно, подставляя в это выражение 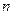 = 1, получаем неопределенность (деление 0 на 0). Если бы в знаменателе (5) вместо
= 1, получаем неопределенность (деление 0 на 0). Если бы в знаменателе (5) вместо 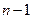 стояло
стояло 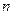 , то разброс получался бы точно равным 0, что бессмысленно.
, то разброс получался бы точно равным 0, что бессмысленно.
Проводя серии измерений одной и той же интересующей нас величины, получим различные выборочные средние значения 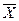 и различные выборочные стандартные отклонения
и различные выборочные стандартные отклонения  . Для оценки точности выборочных оценок используют стандартную ошибку среднего. Она позволяет оценить точность, с которой выборочное среднее характеризует общее среднее значение и носит название стандартной ошибки среднего.
. Для оценки точности выборочных оценок используют стандартную ошибку среднего. Она позволяет оценить точность, с которой выборочное среднее характеризует общее среднее значение и носит название стандартной ошибки среднего.
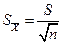 (6)
(6)
Чем больше сделано измерений, тем точнее оценка среднего и тем меньше его стандартная ошибка.
Никогда не следует путать выборочное стандартное отклонение  отдельной серии измерений со стандартной ошибкой общего среднего
отдельной серии измерений со стандартной ошибкой общего среднего 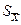 .
.
Если при наличии только приборной погрешности мы практически всегда можем указать интервал, в пределах которого наверняка находится истинное значение измеряемой величины, то при наличии случайной погрешности такой интервал абсолютно точно указать невозможно. Как было отмечено выше, предполагается, что случайные погрешности распределены по нормальному закону (закону Гаусса). Согласно этому закону величина 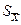 характеризует отклонение
характеризует отклонение 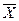 от истинного
от истинного 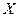 лишь с некоторой вероятностью.
лишь с некоторой вероятностью.
Вводят понятие доверительной вероятности P и доверительного интервала. Доверительная вероятность – это вероятность того, что истинное значение измеряемой величины лежит в некотором заданном доверительном интервале. На практике либо определяют доверительную вероятность при заданном доверительном интервале, либо на оборот, определяют доверительный интервал при заданной доверительной вероятности. Кроме доверительной вероятности используют «противоположное понятие» уровень значимости или вероятность ошибки 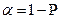 . В медицинских исследованиях чаще всего задается доверительная вероятность P = 0, 95, что соответствует уровню значимости
. В медицинских исследованиях чаще всего задается доверительная вероятность P = 0, 95, что соответствует уровню значимости
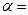 0, 05.
0, 05.
Нормальный закон распределения Гаусса дает возможность определить доверительную вероятность и доверительный интервал при достаточно большом числе измерений (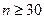 ).
).
На практике чаще проводят меньшее число измерений. В этом случае применяют распределение Стьюдента. Это распределение при (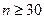 ) практически совпадает с нормальным распределением Гаусса. Распределение Стьюдента дает возможность определить, так называемый, коэффициент Стьюдента
) практически совпадает с нормальным распределением Гаусса. Распределение Стьюдента дает возможность определить, так называемый, коэффициент Стьюдента 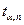 – некоторое число, на которое нужно умножить стандартную ошибку среднего
– некоторое число, на которое нужно умножить стандартную ошибку среднего 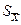 , чтобы получить полуширину доверительного интервала. Индекс
, чтобы получить полуширину доверительного интервала. Индекс 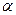 в коэффициенте Стьюдента
в коэффициенте Стьюдента 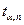 соответствует заданному уровню значимости, а индекс
соответствует заданному уровню значимости, а индекс 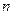 - числу измерений. Коэффициенты Стьюдента находят с помощью соответствующих таблиц (см. приложение 2). Таким образом, найдя по таблице коэффициент Стьюдента, при заданных: уровне значимости α и числу проведенных измерений n, и, рассчитав стандартную ошибку среднего
- числу измерений. Коэффициенты Стьюдента находят с помощью соответствующих таблиц (см. приложение 2). Таким образом, найдя по таблице коэффициент Стьюдента, при заданных: уровне значимости α и числу проведенных измерений n, и, рассчитав стандартную ошибку среднего 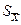 , определяем полуширину доверительного интервала
, определяем полуширину доверительного интервала
∆X ин = 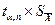 . (7)
. (7)
Оценку точности измерений принято характеризовать относительной погрешностью
δ = 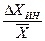 . Ее иногда выражают в процентах.
. Ее иногда выражают в процентах.
Окончательная запись результата измерений должна иметь вид:
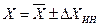 ;
; 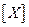 ; P; δ (8)
; P; δ (8)
Где указаны:
1.среднее значение - 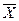 ;
;
2.полуширина доверительного интервала - 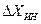 ;
;
3.единицы измерения - 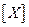 ;
;
4.доверительная вероятность - P;
5.относительная погрешность - δ.
Т.е. мы не можем наверняка, а лишь с некоторой вероятностью утверждать, что истинное значение измеряемой величины лежит в интервале 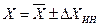 .
.
Напомним еще раз, что такая запись результата справедлива в том случае, когда приборной погрешностью можно пренебречь.
Пример 3.
В результате проведения эксперимента были получены 9 экспериментальных данных:
X 1 = 42,61; x 2 = 44,29; x 3 = 43,18; x4 = 43,93; x5 = 46,70; x6 = 46,45; x 7 = 44,40; x 8 = 41,76; x9 = 46,21
Не трудно видеть, что приборная погрешность(0,005) более чем в 5 раз меньше случайной погрешности. Следовательно, приборную погрешность в этом случае можно не учитывать. Для оценки случайной погрешности составим следующую табл1
| N | 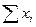
| 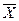
| |||||||||
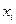
| 42.61 | 44.29 | 43.18 | 43.93 | 46.70 | 46.45 | 44.40 | 41.76 | 46.21 | 399.549 | 44.394 |
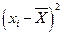
| 3.179 | 0.011 | 1.464 | 0.215 | 5.336 | 4.22 | 3.855E-5 | 6.922 | 3.312 | 24.659 |
По данным табл.1 рассчитаем выборочное стандартное отклонение
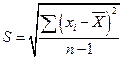
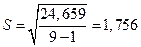 (9)
(9)
Действительно убеждаемся, что S много больше приборной погрешности.
Пусть в рассматриваемом примере задана доверительная вероятность Р = 0,95; (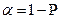 )
)
α = 0,05 и требуется найти доверительный интервал. При заданном уровне значимости α = 0,05 и числу измерений n = 9 по табл. (см. приложение 2) находим коэффициент Стьюдента 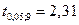 . Найдя стандартную ошибку среднего
. Найдя стандартную ошибку среднего 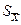 =
= 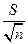 , определяем полуширину доверительного интервала.
, определяем полуширину доверительного интервала.
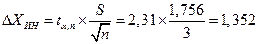 (10)
(10)
Погрешности обычно выражаются одной значащей цифрой и лишь в особо ответственных измерениях двумя. Среднее значение округляется до цифры, разряд которой равен разряду значащей цифры погрешности (ноль не является значащей цифрой). Если отбрасываемая цифра старшего разряда меньше 5, то оставшиеся цифры не изменяются. Если указанная цифра больше или равна 5, то последняя оставшаяся цифра увеличивается на 1. Округление погрешностей проводится по иному. Если округлять погрешности так же, как округляют средние значения, то самопроизвольно возможно уменьшение реальной погрешности. Например, погрешность, рассчитанная по выражению (10), оказалась равной 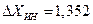 . Округляя ее, как округляют средние значения, получим
. Округляя ее, как округляют средние значения, получим 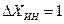 . Т.е. мы самопроизвольно уменьшили реальный доверительный интервал. Поэтому, если отбрасываемая цифра больше или равна 3, то последняя оставляемая цифра увеличивается на 1 (лучше недооценить точность измерений, чем переоценить их).
. Т.е. мы самопроизвольно уменьшили реальный доверительный интервал. Поэтому, если отбрасываемая цифра больше или равна 3, то последняя оставляемая цифра увеличивается на 1 (лучше недооценить точность измерений, чем переоценить их).
В нашем случае окончательный результат должен быть записан так:
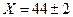 ; P = 0,95 (
; P = 0,95 (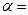 0,05); δ =3%
0,05); δ =3%
Видоизменим рассматриваемый пример.
Пусть теперь при заданной другой полуширине доверительного интервала ∆X ин = 0,48 надо определить доверительную вероятность Р.
Из выражения (7) определяем коэффициент Стьюдента t α.9 = 0,82. По той же табл.
(см. приложение 2) находим доверительную вероятность Р = 0,56.
Окончательный результат при этом будет выглядеть так:
X = 44, 4 ± 0, 5 P = 0, 56 (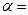 0, 44); δ = 1%
0, 44); δ = 1%
Обратите внимание: значения 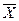 и
и 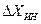 должны быть записаны с одинаковой точностью.
должны быть записаны с одинаковой точностью.
Пример 4.
Округление результатов измерений.
| Запись после округления | |
| 123357 ± 678 | 123400 ±700 |
| 237,46 ± 0,13 | 237, 5 ± 0,2 |
| 0,00283 ± 0,00034 | 0,0028 ± 0,0004 |
| 1,045 ± 0,000003 | 1,045000 ± 0,000003 |
| 359623 ± 307 | 359600 ± 300 |
| 0,0000047 ± 0,0000098 | 0,00005 ± 0,00001 |
| 589 ± 0,69 | 589,0 ± 0,7 |
Еще видоизменим пример.
Пусть заданы и доверительная вероятность Р = 0,98 и полуширина доверительного интервала 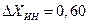 . Требуется определить, сколько надо сделать измерений, чтобы при заданной доверительной вероятности истинное значение случайной величины находилось в заданном доверительном интервале.
. Требуется определить, сколько надо сделать измерений, чтобы при заданной доверительной вероятности истинное значение случайной величины находилось в заданном доверительном интервале.
По табл. (см. приложение 2) при доверительной вероятности Р = 0,98 находим значение коэффициента Стьюдента t 0,02;9 = 2,90 и из выражения 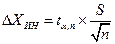 находим n = 72.
находим n = 72.
Если такое число измерений проделать невозможно, то надо изменить методику измерений с целью уменьшения разбросов результатов отдельных измерений.
Напомним еще раз, что в этом примере мы не учитывали приборную погрешность, так как она была на много меньше случайной. Но если приборная погрешность 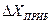 соизмерима со случайной
соизмерима со случайной 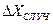 (различаются менее чем в 5 раз), то общая погрешность
(различаются менее чем в 5 раз), то общая погрешность 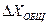 будет складываться из приборной и случайной. В теории погрешности (см. приложение 1) доказывается, что сложение при этом будет не простое (арифметическое), а, так называемое, «квадратическое».
будет складываться из приборной и случайной. В теории погрешности (см. приложение 1) доказывается, что сложение при этом будет не простое (арифметическое), а, так называемое, «квадратическое».
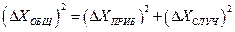
или: 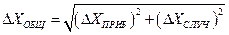 (11)
(11)
В ряде случаев, когда не требуется большая точность, (например, в лабораторных работах) в целях упрощения, применяют простое арифметическое сложение случайной и приборной погрешностей, называя такую предельной погрешностью.
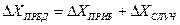 (12)
(12)
Понятно, что она всегда будет несколько больше «квадратической».
Пример 5
В результате проведения эксперимента были получены 9 экспериментальных данных, представленные в таблице (первая строка). Как видно, приборная погрешность равна 0, 05. Оценим случайную погрешность.
| N | 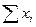
| 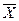
| |||||||||
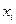
| 45.40 | 45.20 | 45.00 | 44.60 | 44.80 | 44.70 | 44.90 | 45.50 | 45.10 | 405.153 | 45.017 |
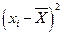
| 0.136 | 0.018 | 1.298E-4 | 0.159 | 0.049 | 0.125 | 6.912E-3 | 0.242 | 5.36E-3 | 0.742 |
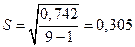
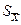 =
= 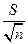 = 0,102
= 0,102
Пусть в рассматриваемом примере задана та же доверительная вероятность Р = 0,95; (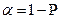 )
)
α = 0,05 и требуется найти доверительный интервал. При заданном уровне значимости α = 0,05 и числу измерений n = 9 по табл. (см. приложение 2) находим коэффициент Стьюдента 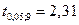 . Найдя стандартную ошибку среднего
. Найдя стандартную ошибку среднего 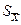 =
= 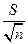 , определяем полуширину доверительного интервала.
, определяем полуширину доверительного интервала.
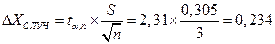
Отношение 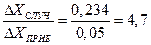 , что меньше 5, и необходимо учитывать и приборную и случайную погрешности. Проведем эту оценку. По выражению (11) она равна:
, что меньше 5, и необходимо учитывать и приборную и случайную погрешности. Проведем эту оценку. По выражению (11) она равна:
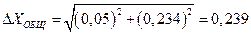 ;
; 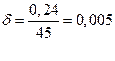
С учетом округления 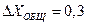 ;
; 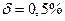
По выражению (12) предельная погрешность будет равна:
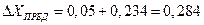
С учетом округления 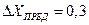
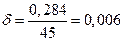
В первом случае запись окончательного результата будет выглядеть так:
X = 45, 0 ± 0, 3; P = 0, 95; δ = 0, 5%
Во втором случае:
X = 45, 0 ± 0, 3; P = 0, 95; δ = 0, 6%
Как видим, окончательные результаты измерений отличаются всего на 0,1%
4. Погрешности косвенных измерений.
При косвенных измерениях, интересующая нас величина рассчитывается по математическим формулам, т.е., она является функцией от соответствующих аргументов, которые непосредственно измеряются в ходе проведения эксперимента. В основе лежит представление о том, что приращение функции приблизительно равно ее дифференциалу.
∆y ≈ d y
Т.е. нахождение погрешности косвенных измерений сводится к нахождению дифференциала функции. Для функции одной переменной это не представляет трудности, однако для функции двух и более переменных несколько усложняется.
В качестве примера определим погрешность при определении объема шара. Наиболее просто измерить диаметр шара, а его объем рассчитать по известной формуле.
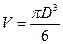 (13)
(13)
Измеряя диаметр, мы совершаем ошибку и, следовательно, объем шара будет содержать погрешность. Объем шара есть функция его диаметра. Напомним, что дифференциал функции равен произведению ее производной на дифференциал аргумента.
d V = 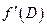 d D
d D
Найдем производную 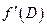 =
= 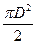 , тогда d V =
, тогда d V = 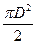 d D
d D
Или, предполагая, d D = ∆D; d V = ∆V имеем: ∆V = 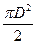
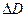
В общем случае, в погрешность ∆V входят приборная и случайная погрешности. Эти погрешности мы уже научились оценивать. Пусть измерение диаметра шара проводилось с помощью штангенциркуля 6 раз и получены одинаковые значения D = 21,70 мм (рис.2)
(т.е. случайные погрешности можно не учитывать). Объем шара при этом
V = 5347,584 мм 3. Приборная погрешность равна 0,05мм (половина цены деления).
D = (21, 70 ± 0, 05), мм
Таким образом, косвенная погрешность в определении объема шара будет равна
∆V = 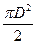
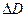 ∆V = 36,96 [мм3]
∆V = 36,96 [мм3]
Относительная погрешность или точность измерения при этом равна
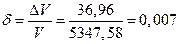 или 0,7%, что является достаточно точным измерением.
или 0,7%, что является достаточно точным измерением.
Окончательно, с учетом округления, получим:
V = (5350 ± 40) мм 3; δ= 0, 7 %
В случае функции двух и более переменных полный дифференциал выражается через частные производные.
Z = Z(x, y)
DZ = 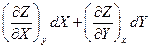
Выражения получаются очень громоздкими. Однако существует метод, позволяющий существенно упростить вычисления. Вместо того чтобы искать абсолютную погрешность находят сначала относительную. Для этого заданную зависимость сначала логарифмируют, а затем полученное выражение дифференцируют. Пусть Z = X*Y тогда 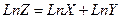
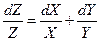 или для конечных приращений
или для конечных приращений 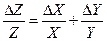 . Абсолютную погрешность находят, умножая найденную относительную, на Z.
. Абсолютную погрешность находят, умножая найденную относительную, на Z. 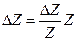 .
.
Рассмотрим это на примере конкретной лабораторной работы.
«Определение коэффициента поверхностного натяжения жидкости».
В этой работе измеряют силу отрыва кольца и его диаметр. Выражение для определения коэффициента поверхностного натяжения имеет вид:
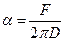 (14)
(14)
Для измерения силы в лаб. работе используются торсионные весы, позволяющие определять силу с точностью в 1 мГ (приборная погрешность). Проведя 5 измерений силы, получим разброс значений сил, существенно превосходящий приборную погрешность. Оценку случайной погрешности в измерении силы при заданной доверительной вероятности (Р = 0,95) проведем рассмотренным ранее способом.
| № измерений | Σ | Среднее значение | |||||
| F, мГ | 404,4 | ||||||
| (∆F)2,(мГ)2 | 243,36 | 31,36 | 207,36 | 19,36 | 5,76 | 507,2 |
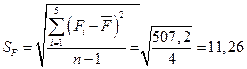
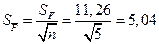
При заданной доверительной вероятности Р = 0, 95 и числу измерений n = 5 находим по таблице (см. приложение 2) коэффициент Стьюдента 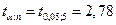 .
.
Находим ∆ F = 2,78*5,04 = 14,01 мГ
Полученный результат будет выглядеть так:
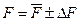
F= (404,4 ± 14,01), мГ; Р = 0, 95; 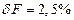
Или, с учетом округления
F= (400 ± 20), мГ; Р = 0, 95; 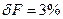 ,
,
Измерения диаметра кольца проводились с помощью штангенциркуля. Получены одинаковые значения D = 10,25 ± 0,05[мм] (приборная погрешность равна 0,05, случайной - пренебрегаем)
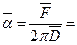 6,37 [мГ/мм] = 62,43 [мН/м]; (1мГ=9,8 10 - 6 Н)
6,37 [мГ/мм] = 62,43 [мН/м]; (1мГ=9,8 10 - 6 Н)
Прологарифмируем выражение (14)
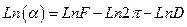
Полученное выражение продифференцируем.
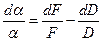
Дифференциалы «d» заменим на конечные приращения «∆» и знаки минус перед «∆» на плюс.
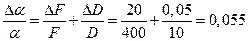
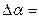 62,43 * 0,055 = 3,4
62,43 * 0,055 = 3,4
δ = 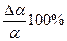 = 6 %
= 6 %
Окончательный результат с учетом округления:
α = (62 ± 4), мН/м; Р = 0, 95; δα = 6%
Таким образом, для оценки погрешности результата косвенного измерения, необходимо:
1.Заданное выражение прологарифмировать.
2.Полученное выражение продифференцировать.
3. Дифференциалы «d» заменить конечными приращения «∆». Эти приращения
задаются либо приборной погрешностью, либо в результате обработки случайных
погрешностей.
4.Перед всеми приращениями «∆» знаки минус заменить плюсом.
5. Полученную относительную погрешность δ умножаем на среднее значение и получаем
абсолютную погрешность «∆».
6.Записываем окончательный результат измерений с учетом округления.






