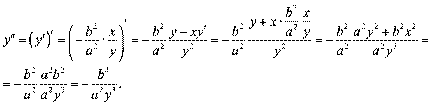“аблиц€ пох≥дних основних функц≥й
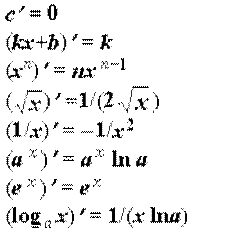
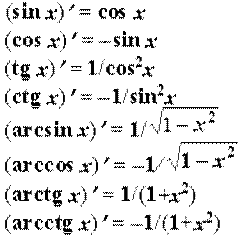

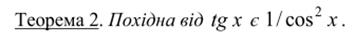

ѕќ’≤ƒЌј ‘”Ќ ÷≤ѓ,ўќ «јƒјЌј Ќ≈я¬Ќќ

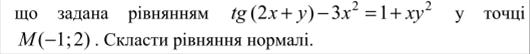




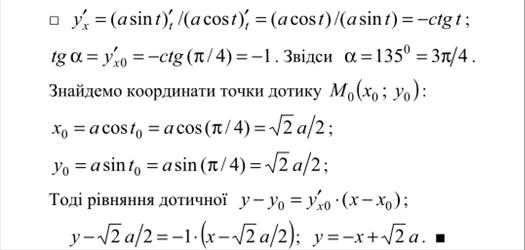
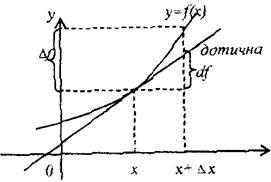
ќзначенн€ диференц≥ала функц≥њ, його геометричний зм≥ст
Ќехай функц≥€ 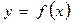 диференц≥йована на в≥др≥зку [a, b]. «а означенн€м пох≥дноњ функц≥њ
диференц≥йована на в≥др≥зку [a, b]. «а означенн€м пох≥дноњ функц≥њ 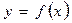 в точц≥ х:
в точц≥ х: 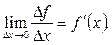
ќск≥льки 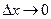 , то
, то 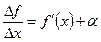 , де
, де 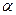 - неск≥нченно мала величина.
- неск≥нченно мала величина.
ћаЇмо: 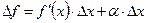 .
.
 ¬еличину
¬еличину 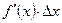 (при
(при 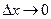 ) називають диференц≥алом функц≥њ
) називають диференц≥алом функц≥њ 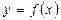 ≥ позначають
≥ позначають 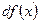 або
або 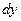 .
.
ƒиференц≥алом функц≥њ 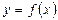 в точц≥ х називаЇтьс€ добуток пох≥дноњ функц≥њ в ц≥й точц≥ на прир≥ст аргументу:
в точц≥ х називаЇтьс€ добуток пох≥дноњ функц≥њ в ц≥й точц≥ на прир≥ст аргументу: 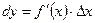 або
або 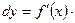
ƒиференц≥ал функц≥њ 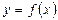 , що в≥дпов≥даЇ значенню х ≥
, що в≥дпов≥даЇ значенню х ≥ 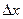 , Ї приростом ординати дотичноњ до граф≥ка функц≥њ
, Ї приростом ординати дотичноњ до граф≥ка функц≥њ 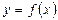 в точц≥ х.
в точц≥ х. 
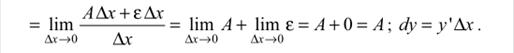

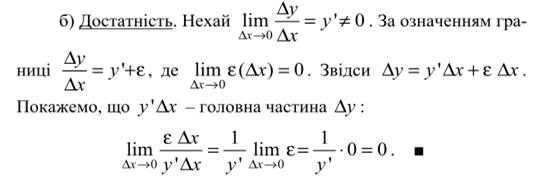







“ема:ѕох≥дн≥ ≥ диференц≥али вищих пор€дк≥в
ѕох≥дн≥ вищих пор€дк≥в
Ќехай на 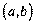 ≥снуЇ пох≥дна
≥снуЇ пох≥дна 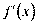 , €ка, в свою чергу, Ї диференц≥йованою на
, €ка, в свою чергу, Ї диференц≥йованою на 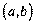 .
.
ќзначенн€ 1. ѕох≥дна в≥д пох≥дноњ першого пор€дку, тобто 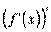 , називаЇтьс€ пох≥дною другого пор€дку або другою пох≥дною функц≥њ
, називаЇтьс€ пох≥дною другого пор€дку або другою пох≥дною функц≥њ 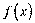 ≥ позначаЇтьс€
≥ позначаЇтьс€ 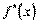 ,
, 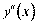 ,
, 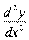 ,
, 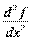 . ќтже,
. ќтже, 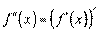 або
або 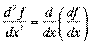 .
.
якщо на 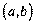 ≥снуЇ
≥снуЇ 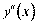 , €ка, в свою чергу, Ї диференц≥йовною на
, €ка, в свою чергу, Ї диференц≥йовною на 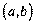 , то пох≥дна третього пор€дку функц≥њ
, то пох≥дна третього пор€дку функц≥њ 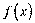 на
на 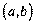 це
це 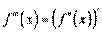 .
.
јналог≥чно, пох≥дна четвертого пор€дку 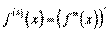 ≥ так дал≥. ѕох≥дна
≥ так дал≥. ѕох≥дна 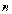 -го пор€дку функц≥њ
-го пор€дку функц≥њ 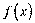 на
на 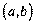
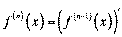 .
.
ќзначенн€ 2. ‘ункц≥€, €ка маЇ пох≥дну 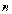 -го пор€дку
-го пор€дку 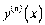 на
на 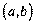 (
(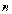 -у пох≥дну) називаЇтьс€
-у пох≥дну) називаЇтьс€ 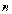 раз диференц≥йовною на
раз диференц≥йовною на 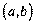 . якщо ж
. якщо ж 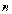 -а пох≥дна
-а пох≥дна 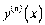 Ї ще й неперервною на
Ї ще й неперервною на 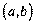 , то функц≥€
, то функц≥€ 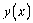 називаЇтьс€
називаЇтьс€ 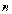 раз неперервно диференц≥йовною на
раз неперервно диференц≥йовною на 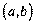 .
.
” загальному випадку дл€ обчисленн€ пох≥дноњ вищого пор€дку потр≥бно знайти спочатку пох≥дн≥ вс≥х нижчих пор€дк≥в. ¬ окремих випадках вдаЇтьс€ встановити загальний вираз дл€ пох≥дноњ 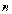 -го пор€дку.
-го пор€дку.
«найти пох≥дну 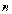 -го пор€дку дл€ наступних функц≥й.
-го пор€дку дл€ наступних функц≥й.
1. 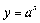 ;
; 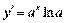 ;
; 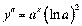 ;
; 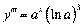 ; Е;
; Е;
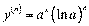 або
або 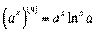 .
.
«окрема, €кщо 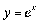 , то
, то 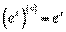 .
.
2. 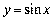 ;
; 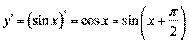 ;
;
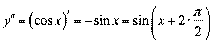 ;
; 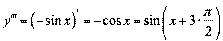 ;
;
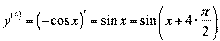 ≥ т.д.
≥ т.д.
ќтже, 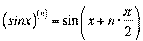 .
.
3. 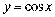 ;
; 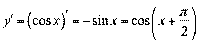 ;
;
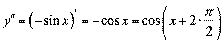 ;
; 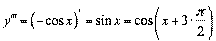
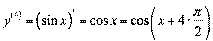 ;
;
≥ т.д.
ќтже,.
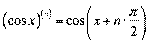
4. 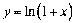 ;
; 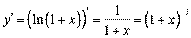 ;
; 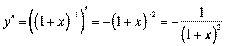 ;
;
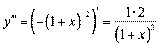 ;
; 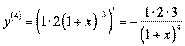 ≥ т.д.
≥ т.д.
ќтже, 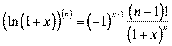 .
.
5. –озгл€немо добуток двох неск≥нченно диференц≥йовних функц≥й 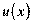 та
та 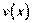 .
.
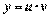 ;
; 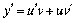 ;
; 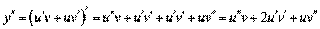 ;
;
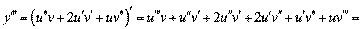
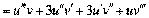 ≥ т.д.
≥ т.д.
«астосувавши метод математичноњ ≥ндукц≥њ можна показати, що
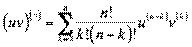 ,
, 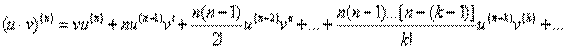
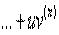
де 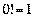 , а пох≥дн≥ нульового пор€дку Ц сам≥ функц≥њ, тобто
, а пох≥дн≥ нульового пор€дку Ц сам≥ функц≥њ, тобто 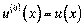 ,
, 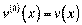 .
.
ќстанн€ формула називаЇтьс€ формулою Ћейбн≥ца дл€ знаходженн€ 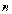 -оњ пох≥дноњ добутку двох неск≥нченно диференц≥йовних функц≥й. ѓњ зручно застосовувати, зокрема, €кщо один ≥з сп≥вмножник≥в Ц многочлен.
-оњ пох≥дноњ добутку двох неск≥нченно диференц≥йовних функц≥й. ѓњ зручно застосовувати, зокрема, €кщо один ≥з сп≥вмножник≥в Ц многочлен.
Ќаприклад, знайти 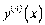 , €кщо
, €кщо 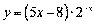 . « формули Ћейбн≥ца маЇмо
. « формули Ћейбн≥ца маЇмо
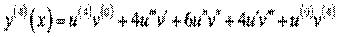 . ” нас
. ” нас 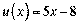 ;
; 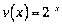 . «найдемо вс≥ потр≥бн≥ пох≥дн≥:
. «найдемо вс≥ потр≥бн≥ пох≥дн≥:
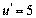 ;
; 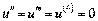 .
.
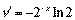 ;
; 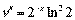 ;
; 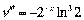 ;
; 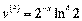 .
.
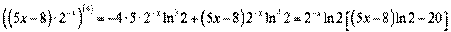
ј тепер розгл€немо пох≥дн≥ вищих пор€дк≥в дл€ параметрично заданих функц≥й. ћаЇ м≥сце теорема.
“еорема 1. якщо функц≥€ 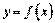 задана параметрично
задана параметрично 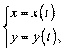
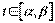 ,
, 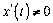 дл€ вс≥х
дл€ вс≥х 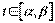 ≥
≥ 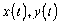 - дв≥ч≥ диференц≥йовн≥, то функц≥€
- дв≥ч≥ диференц≥йовн≥, то функц≥€ 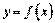 маЇ пох≥дну другого пор€дку, €ку можемо знайти за формулою
маЇ пох≥дну другого пор€дку, €ку можемо знайти за формулою
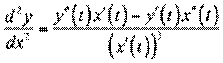 .
.
ƒоведенн€. ¬≥домо, що 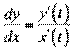 . јле
. јле
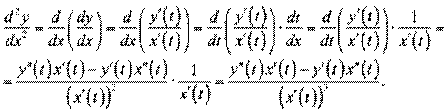
«ауваженн€ 1. ¬с≥ пох≥дн≥ пор€дку 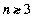 параметрично заданоњ функц≥њ знаход€ть т≥льки за означенн€м. Ѕ≥льш того, нав≥ть дл€ знаходженн€ пох≥дних 2-го пор€дку часто прост≥ше користуватись означенн€м, н≥ж отриманою формулою, що ≥ показують наступн≥ приклади.
параметрично заданоњ функц≥њ знаход€ть т≥льки за означенн€м. Ѕ≥льш того, нав≥ть дл€ знаходженн€ пох≥дних 2-го пор€дку часто прост≥ше користуватись означенн€м, н≥ж отриманою формулою, що ≥ показують наступн≥ приклади.
ѕриклад 1.
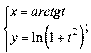
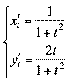 .
.
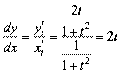 ;
; 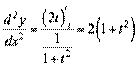 .
.
ѕриклад 2.
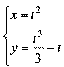 ;
; 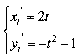 ;
; 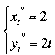 ;
; 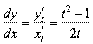 .
.
ƒл€ знаходженн€ другоњ пох≥дноњ використовуЇмо формулу 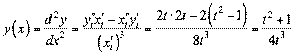 .
.
|
|
|
«ауваженн€ 2. «розум≥ло, що 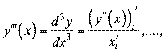
а 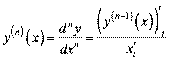 .
.
ѕриклад 3. «найти 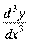 .
.
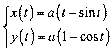
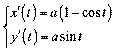
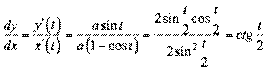 ;
;
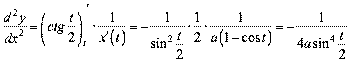 ;
;
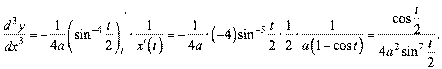
«ауваженн€ 3. ƒл€ не€вно заданих функц≥й також можна знаходити пох≥дн≥ вищих пор€дк≥в. ѕри диференц≥юванн≥ потр≥бно памТ€тати, що зм≥нна 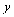 Ї функц≥Їю
Ї функц≥Їю 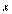 (€к складна), тобто
(€к складна), тобто 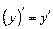 ,
, 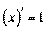 .
.
Ќаприклад, знайти 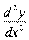 , €кщо
, €кщо 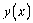 задана р≥вн€нн€м:
задана р≥вн€нн€м:
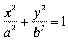 ;
; 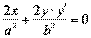 ;
; 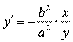 ;
;