г) Молекулярные силы в твердых телах

Твердость тела обусловлена силами сцепления, действующими между молекулами.

Смачиванием называется сцепление между молекулами различных веществ (стекла и воды). Смачиванием объясняется крашение (рисование), склеивание, пайка, никелировка, хромирование и т.п.

Твердостью называется сопротивление тела, которое оно оказывает вдавливанию или царапанью его поверхности.

Шкала твердости (минералогическая):

1.-тальк, 2.- гипс, 3. -известковый шпат, 4.- плавиковый шпат, 5. -апатит, 6. -полевой шпат, 7. -кварц, 8. -топаз, 9. -корунд, 10. -алмаз.

Каждое тело из этой последовательности царапает любое предыдущее.

Тела, которые после растяжения или сжатия восстанавливают свою первоначальную форму, называются упругими; тела, сохраняющие деформацию, - пластическими. Если деформация превышает известный предел (предел упругости), тело не полностью восстанавливает свою форму.

Коэффициент растяжения ε представляет растяжение, возникающее в стержне длиной 1 м с поперечным сечением 2 мм ² при воздействии на него растягивающей силой 1 кп. Коэффициент растяжения ε представляет собой константу вещества; ее обратное значение называется модулем растяжения (Е).

Растяжение d = (ε l P): s

l - длина в метрах, Р - растягивающая сила в килопондах, s - поперечное сечение в кв.мм.

ε = 1: Е (мм/кп),

тогда d получается в метрах.

Предел прочности (на растяжение) представляет собой ту силу, при которой наступает разрыв.

Предел прочности (на раздавливание) представляет собой ту силу, при которой происходит раздавливание

Изгиб и кручение также вызывают упругие силы сопротивления. Для всех упругих сил примени́м закон Гука(1678):

Ниже предела упругости растяжение, сжатие изгиб и кручение пропорциональны деформирующим силам

Технически допустимая нагрузка значительно меньше предела прочности. Запасом прочности называют отношение предела прочности на растяжение или раздавливание к допустимому напряжению.

Вещество	Коэффициент растяжения ε	Предел прочности на растяжение кп/мм2	Предел прочности на раздавливание кп/мм2
сталь железо медь алюминий свинец стекло дуб (параллельно волокнам)	0,000045 0,000053 0,00008 0,00014 0,0006 0,00014 0,0007	70 ± 120 40 ± 60 15 ± 30 17 ± 20 1,4 ± 1,8 0,7 ± 3 6 ± 10	100 ± 300 60 ± 90 28 ± 40 7,5 ± 10 5,4

 

Кинетическая энергия твёрдого тела.

Для твёрдого тела имеет место формула: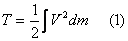

Нужно различать кинетическую энергию твёрдого тела при различных видах его движения.

Кинетическая энергия тела твёрдого движущегося поступательно.

При поступательном движении, все скорости одинаковы. Тогда:

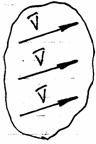
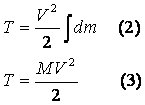
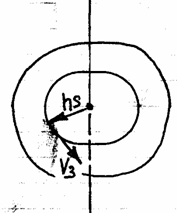
Кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси.

Модуль скорости любого тела, вращающегося вокруг неподвижной оси: .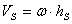

Подставим это в (1):

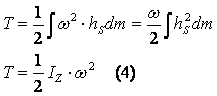
Кинетическая энергия твёрдого тела совершающего плоское движение.

При плоском движении тела, всегда перпендикулярен плоскости движения и совпадают с осью CZ2.

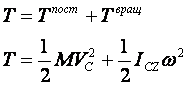
Заключение: если материальная система состоит из нескольких тел, то её кинетическая энергия будет равен сумме всех кинетических энергий.

Теорема об изменении кинетической энергии системы.

Пусть система состоит из n точек, где - равнодействующая внутренних сил, 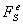- равнодействующая внешних сил.

Теорема об изменения кинетической энергии для S-ой точки в дифференциальной форме.

Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних тел системы.

Теорема в интегральной форме.

Эта теорема для S-ой точки имеет вид: .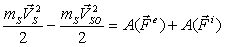

Просуммируем равенство по всем точкам:

Равенство (2) выражает теорему в интегральной форме: изменение кинетической энергии системы на некотором её перемещении, равно сумме работ всех внешних и внутренних сил на этом же перемещении. В случае не изменяемых систем: .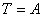

Колебания материально точки подразделяют на свободные и вынужденные. Свободные возникают в результате вывода системы из равновесия и в дальнейшем предоставляют ей возможность колебаться свободно, без приложения внешних сил. Вынужденные - это колебания точки и мех-ой системы, происходящие по действием приложенной к ней периодической, гармонической, вынуждающей силы.