Пример 1. Исследуем на монотонность и экстремумы функцию f (x) = x 3 – 3ln x.
Решение. Функция f (x) определена для всех x > 0, т. е. D (f) = (0; + 
). Производная существует в каждой точке промежутка (0; + ), найдем ее:
= 3 x 2 –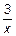 
= 
.
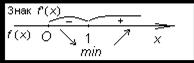
Так как = 0 лишь при x = 1, то функция f (x) имеет единственную критическую точку x = 1. Рис. 22
При x > 1производная положительна, а при x 
(0; 1) — отрицательна, следовательно, на промежутке (0; 1] функция убывает, а на промежутке [1; + ) — возрастает (рис. 22). Точка
x = 1 — точка локального минимума функции. Так как она единственная, то в ней функция достигает своего минимума (наименьшего значения): f (1) = 13 – 3ln 1 = 1.
Ответ. На промежутке (0; 1] функция убывает, на промежутке [1; + ) — возрастает,
наименьшее значение, равное 1, функция достигает в точке x = 1.
Пример 2. Найдем наибольшее и наименьшее значение функции f (x) =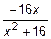 
.
Решение. Функция f (x) определена для всех x R. Производная существует в каждой точке области определения функции, найдем ее:
= 
= 
.
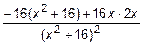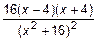Так как = 0 лишь при x = 4 и при x = –4, то функция f (x) имеет две критические точки x = 4 и x = –4. Рис. 23
При x < –4 и при x > 4производная положительна, а при –4 < x < 4 — отрицательна, следовательно, на промежутках (– ; –4] и [4; + ) функция возрастает, а на промежутке
[–4; 4] — убывает (рис. 23). Точка x = –4 — точка локального максимума функции, а точка x = 4 — точка локального минимума.
Так как f (x) = 0 при x = 0, f (x) < 0 при x > 0 и f (x) > 0 при x < 0, то в точке локального минимума x = 4 функция достигает своего наименьшего значения f (4) = –2, а в точке локального максимума x = –4 она достигает своего наибольшего значения f (–4) = 2.
Ответ. max f (x) = f (–4) = 2, min f (x) = f (4) = –2.
Пример 3*. Найдем точки перегиба и промежутки выпуклости (вогнутости) графика функции f (x) = x 3 –3 x 2 + 9 x – 4.
Решение. Функция f (x) определена для всех x R. Производная существует в каждой точке области определения функции, найдем ее:
= (x 3 –3 x 2 + 9 x – 4)′ = 3 x 2 – 6 x + 9.
Найдем вторую производную:
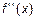= (3 x 2 – 6 x + 9)′ = 6 x – 6.
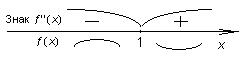
Вторая производная обращается в нуль только в точке x = 1. Определим знак второй производной на каждом из интервалов (– ; 1)
и (1; + ) (рис. 24). Рис. 24
Вторая производная функции f (x) в точке x = 1 меняет знак, следовательно, x = 1 — точка перегиба графика этой функции. На интервале (– ; 1) вторая производная отрицательна, поэтому график функции f (x) имеет выпуклость вверх. На интервале (1; + ) вторая производная положительна, поэтому график функции f (x) имеет выпуклость вниз.
Ответ. Функция выпукла вверх на интервале (– ; 1), выпукла вниз на интервале (1; + ).
