Пример 1. Дана функция f (x) = x 3 – 6 x 2 + 9 x + 7. Найдем:
а) критические точки функции f (x) на отрезке [–2; 2];
б) наибольшее и наименьшее значение функции f (x) на отрезке [–2; 2].
Решение. а) Производная функции f (x) существует для любого x 
R. Найдем ее:
= (x 3 – 6 x 2 + 9 x + 7)′ = 3 x 2 – 12 x + 9.
Найдем точки, в которых = 0. Для этого решим уравнение
3 x 2 – 12 x + 9 = 0. (1)
Уравнение (1) имеет два корня: 1 и 3. Из этих чисел только число 1 является внутренней точкой отрезка [–2; 2]. Поэтому x = 1 — единственная критическая точка функции f (x) на отрезке [–2; 2].
б) Вычислим значения функции f (x) на концах отрезка и в критической точке:
f (–2) = (–2)3 – 6×(–2)2 + 9×(–2) + 7 = –43;
f (1) = 13 – 6×12 + 9×1 + 7 = 11;
f (2) = 23 – 6×22 + 9×2 + 7 = 9.
Наибольшее значение функции f (x) на отрезке [–2; 2] равно 11, это значение достигается в точке x = 1; наименьшее значение функции f (x) на отрезке [–2; 2] равно –43, это значение достигается в точке x = –2:
f (x) = f (1) = 11; 
f (x) = f (–2) = –43.
Ответ. а) x = 1; б) f (x) = 11; f (x) = –43.
Пример 2. Дана функция f (x) = x 2 – 3 
. Найдем:
а) критические точки функции f (x) на отрезке [–1; 8];
б) наибольшее и наименьшее значение функции f (x) на отрезке [–1; 8].
Решение. Производная функции f (x) существует для любого x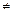 
0 (см. п. 13). Следовательно, она существует в любой точке отрезка [–1; 8], кроме точки x = 0. Поэтому x = 0 — критическая точка функции f (x) на отрезке [–1; 8].
Для любого x 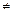0 найдем производную функции f (x): = 2 x – 
.
Найдем точки, в которых = 0. Для этого решим уравнение
2 x – = 0. (2)
Уравнение (2) имеет два корня: 1 и –1. Из этих чисел только число 1 является внутренней точкой отрезка [–1; 8]. Поэтому x = 1 — еще одна критическая точка функции f (x) на отрезке [–1; 8].
Итак, функция f (x) на отрезке [–1; 8] имеет две критические точки: x = 0 и x = 1.
б) Для нахождения наибольшего и наименьшего значения функции на отрезке вычислим ее значения на концах отрезка и в каждой критической точке:
f (–1) = (–1)2 – 3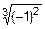 
= –2;
f (0) = 02 – 3 
= 0;
f (1) = 12 – 3 
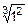= –2;
f (8) = 82 – 3 
= 52.
Итак, 
f (x) = f (8) = 52,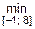 
f (x) = f (–1) = f (1) = –2.
Ответ. а) x = 0 и x = 1; б) f (x) = 52, 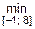f (x) = –2.
Пример 3. Найдем наибольшее и наименьшее значение функции f (x) = x 5 – 10 x 3 + 50 x – 10 на отрезке [–1; 1].
Решение. Производная функции f (x) существует для любого x R. Найдем ее:
= (x 5 – 10 x 3 + 50 x – 10)′ = 5 x 4 – 30 x 2 + 50.
Производная функции f (x) не обращается в нуль ни для какого x, так как 5 x 4 – 30 x 2 + 50 =
= 5(x 4 – 6 x 2 + 9) + 5 = 5(x 2 – 3)2 + 5 > 0 для любого действительного числа x. Следовательно, функция f (x) не имеет критических точек, наибольшее и наименьшее значение на отрезке
[–1; 1] она достигает на концах этого отрезка.
Вычислим значения функции f (x) на концах отрезка:
f (–1) = (–1)5 – 10×(–1)3 + 50×(–1) – 10 = –51;
f (1) = 15 – 10×13 + 50×1 – 10 = 31;
Итак, 
f (x) = f (1) = 31, 
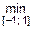f (x) = f (–1) = –51.
Ответ. f (x) = 31, 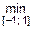f (x) = –51.
