Пример 1. Дана функция f (x) = 3 x 2 + 4 x – 5. Напишем уравнение касательной к графику функции f (x) в точке графика с абсциссой x 0 = 1.
Решение. Производная функции f (x) существует для любого x 
R. Найдем ее:
= (3 x 2 + 4 x – 5)′ = 6 x + 4.
Тогда f (x 0) = f (1) = 2; 
(x 0) = 
= 10. Уравнение касательной имеет вид:
y = (x 0) (x – x 0) + f (x 0),
y = 10(x – 1) + 2,
y = 10 x – 8.
Ответ. y = 10 x – 8.
Пример 2. Дана функция f (x) = x 3 – 3 x 2 + 2 x + 5. Напишем уравнение касательной к графику функции f (x), параллельной прямой y = 2 x – 11.
Решение. Производная функции f (x) существует для любого x R. Найдем ее:
= (x 3 – 3 x 2 + 2 x + 5)′ = 3 x 2 – 6 x + 2.
Так как касательная к графику функции f (x) в точке с абсциссой x 0 параллельна прямой y = 2 x – 11, то ее угловой коэффициент равен 2, т. е. (x 0) = 2. Найдем эту абсциссу из условия, что 3 x 
– 6 x 0 + 2 = 2. Это равенство справедливо лишь при x 0 = 0 и при x 0 = 2. Так как в том и в другом случае f (x 0) = 5, то прямая y = 2 x + b касается графика функции или в точке (0; 5), или в точке (2; 5).
В первом случае верно числовое равенство 5 = 2×0 + b, откуда b = 5, а во втором случае верно числовое равенство 5 = 2×2 + b, откуда b = 1.
Итак, существует две касательные y = 2 x + 5 и y = 2 x + 1 к графику функции f (x), параллельные прямой y = 2 x – 11.
Ответ. y = 2 x + 5, y = 2 x + 1.
Пример 3. Дана функция f (x) = x 2 – 6 x + 7. Напишем уравнение касательной к графику функции f (x), проходящей через точку A (2; –5).
Решение. Так как f (2)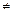 
–5, то точка A не принадлежит графику функции f (x). Пусть x 0 — абсцисса точки касания.
Производная функции f (x) существует для любого x R. Найдем ее:
= (x 2 – 6 x + 1)′ = 2 x – 6.
Тогда f (x 0) = x – 6 x 0 + 7; (x 0) = 2 x 0 – 6. Уравнение касательной имеет вид:
y = (2 x 0 – 6)(x – x 0) + x – 6 x 
+ 7,
y = (2 x 0 – 6) x – x + 7.
Так как точка A принадлежит касательной, то справедливо числовое равенство
–5 = (2 x 0 – 6)×2– x + 7,
откуда x 0 = 0 или x 0 = 4. Это означает, что через точку A можно провести две касательные к графику функции f (x).
Если x 0 = 0, то уравнение касательной имеет вид y = –6 x + 7. Если x 0 = 4, то уравнение касательной имеет вид y = 2 x – 9.
Ответ. y = –6 x + 7, y = 2 x – 9.
Пример 4. Даны функции f (x) = x 2 – 2 x + 2 и g (x) = – x 2 – 3. Напишем уравнение общей касательной к графикам этих функции.
Решение. Пусть x 1 — абсцисса точки касания искомой прямой с графиком функции f (x), а x 2 — абсцисса точки касания той же прямой с графиком функции g (x).
Производная функции f (x) существует для любого x R. Найдем ее:
= (x 2 – 2 x + 2)′ = 2 x – 2.
Тогда f (x 1) = x 
– 2 x 1 + 2; (x 1) = 2 x 1 – 2. Уравнение касательной имеет вид:
y = (2 x 1 – 2)(x – x 1) + x – 2 x 1 + 2,
y = (2 x 1 – 2) x – x + 2. (1)
Найдем производную функции g (x):
= (– x 2 – 3)′ = –2 x.
Тогда g (x 2) = – x 
– 3;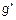 
(x 2) = –2 x 2. Уравнение касательной имеет вид:
y = –2 x 2 (x – x 2) – x – 3,
y = –2 x 2 x + x – 3. (2)
Очевидно, что уравнения (1) и (2) являются уравнениями одной и той же прямой при выполнении двух условий: 2 x 1 – 2 = –2 x 2 и – x + 2 = x – 3. Решив систему двух уравнений с двумя неизвестными x 1 и x 2, получим или x 1 = 2, x 2 = –1, или x 1 = –1, x 2 = 2. Это означает, что существует две общие касательные к графикам функций f (x) и g (x). Подставив x 2 = –1, затем x 2 = 2 в уравнение (2), получим уравнения двух касательных: y = 2 x – 2 и y = –4 x + 1.
Ответ. y = 2 x – 2, y = –4 x + 1.
