Для разных направлений в заданной точке поверхности получается разная кривизна нормального сечения, которая называется нормальной кривизной; ей приписывается знак плюс, если главная нормаль кривой идёт в том же направлении, что и нормаль к поверхности, или минус, если направления нормалей противоположны.
Вообще говоря, в каждой точке поверхности существуют два перпендикулярных направления 
и 
, в которых нормальная кривизна принимает минимальное и максимальное значения; эти направления называются главными. Исключение составляет случай, когда нормальная кривизна по всем направлениям одинакова (например, у сферы или на торце эллипсоида вращения), тогда все направления в точке — главные.
Поверхности с отрицательной (слева), нулевой (в центре) и положительной (справа) кривизной.
Нормальные кривизны в главных направлениях называются главными кривизнами; обозначим их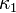 
и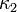 
. Величина:
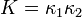
называется гауссовой кривизной, полной кривизной или просто кривизной поверхности. Встречается также термин скаляр кривизны, который подразумевает результатсвёртки тензора кривизны; при этом скаляр кривизны вдвое больше, чем гауссова кривизна.
Гауссова кривизна может быть вычислена через метрику, и поэтому она является объектом внутренней геометрии поверхностей (отметим, что главные кривизны к внутренней геометрии не относятся). По знаку кривизны можно классифицировать точки поверхности (см. рисунок). Кривизна плоскости равна нулю. Кривизна сферы радиуса R всюду равна 
. Существует и поверхность постоянной отрицательной кривизны — псевдосфера.
[править] Геодезические линии, геодезическая кривизна
Основная статья: Геодезическая
Кривая на поверхности называется геодезической линией, или просто геодезической, если во всех её точках главная нормаль к кривой совпадает с нормалью к поверхности. Пример: на плоскости геодезическими будут прямые и отрезки прямых, на сфере — большие круги и их отрезки.
Эквивалентное определение: у геодезической линии проекция её главной нормали на касательную плоскость есть нулевой вектор. Если кривая не является геодезической, то указанная проекция ненулевая; её длина называется геодезической кривизной 
кривой на поверхности. Имеет место соотношение:
,
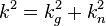где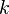 
— кривизна данной кривой, 
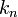— кривизна её нормального сечения с той же касательной.
Геодезические линии относятся к внутренней геометрии. Перечислим их главные свойства.
· Через данную точку поверхности в заданном направлении проходит одна и только одна геодезическая.
· На достаточно малом участке поверхности две точки всегда можно соединить геодезической, и притом только одной. Пояснение: на сфере противоположные полюса соединяет бесконечное количество меридианов, а две близкие точки можно соединить не только отрезком большого круга, но и его дополнением до полной окружности, так что однозначность соблюдается только в малом.
· Геодезическая является кратчайшей. Более строго: на малом куске поверхности кратчайший путь между заданными точками лежит по геодезической.
