Касательная плоскость в точке поверхности.
Касательная плоскость в точке гладкой поверхности — это плоскость, имеющая максимальный порядоксоприкосновения с поверхностью в этой точке. Эквивалентный вариант определения: касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку.
Пусть гладкая кривая на параметрически заданной поверхности 
задана в виде:
.
Направление 
касательной к такой кривой даёт вектор:
Отсюда видно, что все касательные ко всем кривым в данной точке лежат в одной плоскости, содержащей векторы 
, которые мы выше предположили независимыми.
Уравнение касательной плоскости в точке 
имеет вид:
(смешанное произведение векторов).
В координатах уравнения касательной плоскости для разных способов задания поверхности приведены в таблице:
касательная плоскость к поверхности в точке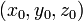 
| |
| неявное задание |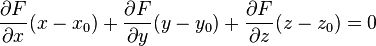 
|
| явное задание | 
|
| параметрическое задание | 
|
Все производные берутся в точке .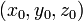
