Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если f(a) = f(b) то внутри интервала [а, b] найдется хотя бы одно такое значение x0 (a < x0 < b), что f ' (x0) = 0.
Доказательство. Рассмотрим два случая.
1. Функция f(x) постоянна на интервале [а, b]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически.
2. Функция f(x) не является постоянной (Рисунок 1); тогда наибольшего или наименьшего или обоих этих значений она достигает во внутренней точке интервала, ибо f(b) = f(a), и если f(a) - наименьшее значение, то наибольшее значение значение функция f(x) примет внутри интервала.
Рис.1  Рис.2
Рис.2 
Пусть например f(x0) - наибольшее значение функции f(x) на интервале [а, b] и x0 - внутренняя точка этого интервала. Тогда f(x0) является максимумом функции: f(x0) і f(x) для всех x из достаточно малой окрестности x0 [за эту окрестность можно впрочем, взять интервал (а, b)].
Так как, по условию, f(x) имеет в точке x0 производную, то по теореме о необходимом признаке экстремума, f ' (x0) = 0, и теорема Ролля доказана.
Теорема Ролля имеет простое геометрическое толкование: если дана дуга AB кривой y = f(x), в каждой точке которой существует касательная, причем концы A и B находятся на одинаковом расстоянии от оси Ox, то на этой дуге найдется по крайней мере одна точка, в которой касательная t к кривой будет параллельна стягивающей дугу хорде, а следовательно и оси Ox (смотри рисунок 1).
Если повернуть оси координат на угол a, то концы A и B дуги AB уже не будут находится на одинаковом расстоянии от оси Ox', но касательная t по прежнему будет параллельна хорде AB (смотри рисунок 1). Поэтому естественно ожидать, что имеет место теорема:
Если дана дуга AB кривой y = f(x) с непрерывно изменяющейся касательной, то на этой дуге найдется хотя бы одна точка, в которой касательная параллельна стягивающей ее хорде AB (Рисунок 2).
Эта теорема является геометрической перефразировкой следующей теоремы, известной под названием теоремы Лагранжа.
Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x0 (a < x0 < b), что f(b) - f(a) = (b - a)f '(x).
Доказательство. Рассмотрим вспомогательную функцию
F(x) = f(x) - k(x - a), где
 - угловой коэффициент хорды AB (смотри рисунок 2).
- угловой коэффициент хорды AB (смотри рисунок 2).
Эта функция удовлетворяет всем условиям теоремы Ролля.
В самом деле, при x = a имеем F(a) = f(a) - k(a - a) = f(a), при x = b имеем 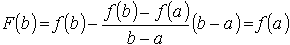
Кроме того, так как функция f(x) и k(x - a) непрерывны на [a, b] и диференцируемы в (a, b), то и функция F(x) = f(x) - k(x - a) непрерывна на [a, b] и диференцируема в (a, b).
Следовательно, по теореме Ролля, в интервале (a, b) найдется такая точка x0, что F'(x0) = 0, т.е. f ' (x0) - k = 0 или
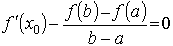
Отсюда имеем
f(b) - f(a) = (b - a)f ' (x0),
что и требовалось доказать.
Так как a + (b - a) = b, то величина a + Q(b - a), где Q - правильная положительная дробь (0 < Q < 1), равна какому-то числу в интервале (a, b), поэтому формулу Лагранжа можно записать в виде
f(b) - f(a) = (b - a)f ' [a + Q(b - a)]
Если положить a = x, b = x + Dx, откуда b - a = Dx, то формула Лагранжа запишется в виде
Dy = f(x + Dx) - f(x) = Dxf ' (x + QDx).
Ранее было доказано, что если функция равна постоянной C при любом значении x в интервале (a, b), то ее производная равна нулю.
Докажем теперь обратную теорему, являющуюся следствием теоремы Лагранжа:
Если производная f ' (x) обращается в нуль для любых значений x в интервале (a, b), то в этом интервале f(x) = C.
В самом деле, если x1 и x2 - два любых значения в интервале (a, b), то в силу теоремы Лагранжа, имеем f(x2) - f(x1) = (x2 - x1)f'(x0), где, x1 < x0 < x2. Но так как f'(x0) = 0, то f(x2) - f(x1) = 0, что и доказывает нашу теорему.
Отсюда непосредственно вытекает важная теорема:
Если две функции f1 (x) и f2 (x) имеют одну и ту же производную в интервале (a, b), то они на данном интервале отличаются друг от друга на постоянную величину.
В самом деле, рассмотрим функцию j(x) = f2(x) - f1(x). Тогда для любого значения x из интервала (a, b) j'(x) = f2'(x) - f1'(x) = 0. Но это означает, что j(x) = C и, следовательно f2(x) - f1(x) = С.






