Вынесение постоянного множителя за знак производной.
Докажем формулу
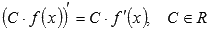
По определению производной имеем: 
Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому
Производная суммы, производная разности.
Для доказательства второго правила дифференцирования
воспользуемся определением производной и свойством предела непрерывной функции.
Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных
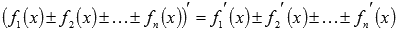
Производная частного двух функций (производная дроби).
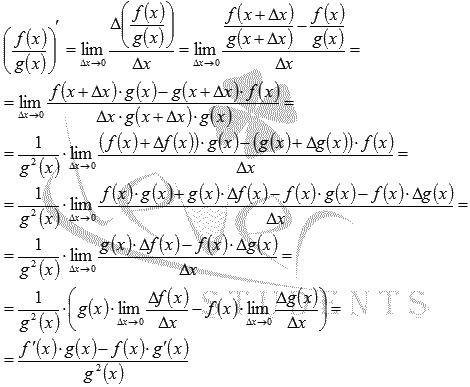
Докажем правило дифференцирования частного двух функций (дроби)
Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.
По определению производной
При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем 
где x – любое действительное число, то есть, x – любое число из области определения функции 
Запишем предел отношения приращения функции к приращению аргумента при 
Следует заметить, что под знаком предела получается выражение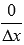 
, которое не является неопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения.
