
В одномерном случае:

Рассмотрим набор узлов x 1, x 2,... x n. Расстояние между соседними узлами равно h:
x j- x j-1= h
 (1)
(1)
Для анализа на устойчивость представим искомую функцию в виде некоторого решения R (x, t) и возмущения ε(x, t):

Поскольку R j(t) - решение, для него выполнено:
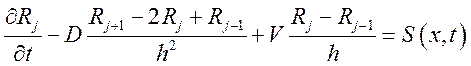
Подставим решение с возмущением в уравнение (1):
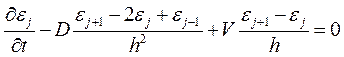 (2)
(2)
Поскольку уравнение линейное однородное, его можно разложить в ряд Фурье. Поэтому рассмотрим одну Фурье-компоненту:

В начальный момент времени:
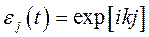
Любое начальное возмущение можно разложить в ряд по таким "элементарным" возмущениям с разными волновыми числами k.
Подставляя "элементарное" возмущение в уравнение (2), получаем:
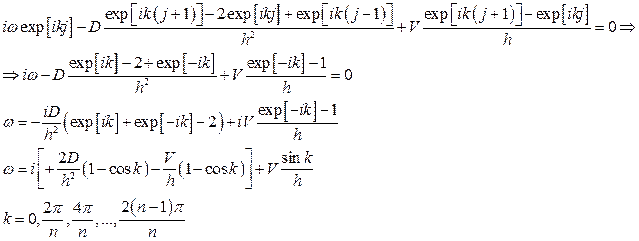
Мнимая часть частоты ω дает экспоненциальный рост, если Im[ω]<0 и экспоненциальное затухание, если Im[ω]< 0. Мы получили:

При этом 1-cos[k]≥0. Так что экспоненциальный рост, означающий возникновение неустойчивости, возникает для любых чисел k, если:

Соответствующее безразмерное число называется числом Пекле Pe:

Если решение оказывается неустойчивым (возникновение отрицательных концентраций), есть два пути:
| Увеличивать коэффициент диффузии D (методы "искусственной диффузии", "искусственной теплопроводности", "искусственной вязкости") | Уменьшать размер элементов h |






