Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.
При этом в процессе поиска семейство хорд может строиться:
) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х0=b (рис. 4.10а);
б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х0=a (рис. 4.10б);
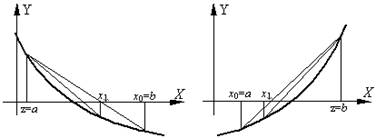
Рис. 4.10.
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:
для случая а)

| (4.11) |
для случая б)
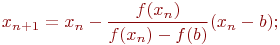
| (4.12) |
Процесс поиска продолжается до тех пор, пока не выполнится условие

| (4.13) |
Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.
Схема алгоритма уточнения корня методом хорд представлена на рис. 4.11.

Рис. 4.11. Схема алгоритма уточнения корня методом хорд






