Определение. Полным приращением функции  в точке М(х;у) называется разность
в точке М(х;у) называется разность 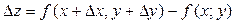 , где
, где  и
и  произвольные приращения аргументов.
произвольные приращения аргументов.
Определение. Функция  называется дифференцируемой в точке М(х;у), если в этой точке полное приращение можно представить в виде
называется дифференцируемой в точке М(х;у), если в этой точке полное приращение можно представить в виде 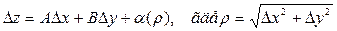 .
.
Определение. Полным дифференциалом функции  называется главная часть полного приращения
называется главная часть полного приращения  , линейная относительно приращений аргументов
, линейная относительно приращений аргументов  и
и  , то есть
, то есть 
Полный дифференциал функции  вычисляется по формуле:
вычисляется по формуле:
 .
.
Для функции трех переменных

При достаточно малом  для дифференцируемой функции
для дифференцируемой функции  справедливы приближенные равенства
справедливы приближенные равенства  , которые применяются для приближенного вычисления значения функции:
, которые применяются для приближенного вычисления значения функции:

Примеры
а) Вычислить приближенное значение функции  в точке М (2,15; 1,25) с помощью полного дифференциала. Ответ сравнить с вычислением на калькуляторе.
в точке М (2,15; 1,25) с помощью полного дифференциала. Ответ сравнить с вычислением на калькуляторе.
Решение.
Используем формулу: 
1.Выберем точку с целыми координатами, ближайшую к М - М0(2;1).
Тогда: 
2. Найдем значение функции в точке М0

3. Вычислим частные производные данной функции и найдем их значения в точке М0
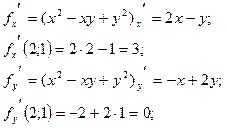
4. Вычислим полный дифференциал и данной функции в точке М0

5. Найдем значение функции в точке М:

6. С помощью калькулятора вычислим точное значение функции в данной точке:

б) С помощью полного дифференциала функции двух переменных вычислить приближенно значение данного выражения. Вычислить это же выражение с помощью микрокалькулятора. 
Решение:
1.Введем функцию 
Тогда: 
2. Найдем значение функции в точке (х0;у0)
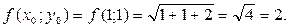
3. Вычислим частные производные данной функции и найдем их значения в точке (х0;у0)

4. Вычислим полный дифференциал и данной функции в точке (х0;у0)

5. Таким образом, приближенное значение данного выражения:

6. Значение, вычисленное с помощью микрокалькулятора: 2,007045533






