2. Уравнения вида: |f(x) |=g(x). Уравнения с одним модулем.
Уравнения такого вида могут быть заданы как угодно, неизменна суть: есть одно выражение с модулем и выражение без модуля.
Уравнение рассматриваемого вида, выражение без модуля проще чем под модулем.
Итак,
1. Приводим уравнение к виду: |f(x) |=g(x):
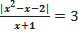→: |х²-х-2|=3(х+1)
2. Учитываем, что g(x)≥0
х+1>0 (строго больше так как х+1 в знаменателе, а знаменатель не равен 0!!!)
3. Решаем совокупность уравнений: 
х²-х-2=3(х+1) → х²-4х-5=0→ х1=-1 и х2=5
х²-х-2=-3(х+1) → х²+2х+1=0→х=-1
Теперь важный момент при решении многих уравнений с модулем: проверяем удовлетворяют ли наши корни условию х+1>0!
Обратите внимание, что я не решаю неравенство, так как чаще всего корни легко проверяются подстановкой и само решение будет лишней тратой времени. Выкидываем посторонний х1=-1
Ответ: х=5.
х²+4х+1=2|х+2|
Здесь, выражение под модулем проще, чем без модуля, следовательно решаем методом интервалов:
1) Найти критические точки, т.е. значение неизвестной, при которых выражение, стоящее под знаком модуля, обращается в нуль; (Каждое выражение, стоящее под знаком модуля, приравнять к 0 и решить уравнение);
х+2=0 → х=-2
2) Расставить полученные точки (корни) на числовой прямой и разбить область допустимых значений уравнения на промежутки, на каждом из которых, выражения, стоящие под знаком модуля сохраняют знак;
• →
① -2 ②
3) На каждом из этих промежутков уравнение записать без знака модуля, а затем решить его.
① x: (-∞; -2)
Заметим, что на этом промежутке, выражение под модулем х+2 всегда принимает отрицательные значения, в этом легко убедиться взяв любое число из рассматриваемого промежутка, например: х=-3 и подставив в модуль: x+2=-3+2<0
Таким образом, на рассматриваемом промежутке: x+2<0→ |х+2|=-x-2 в итоге на этом промежутке исходное уравнение после раскрытия модулей будет иметь вид:
х²+4х+1=2(-х-2) → х²+6х+5=0→х1=-1 и х2=-5;
Не забываем сделать проверку корней,убираем посторонний корень х1=-1, так как он не удовлетворяет условию х+2<0
② х: [-2; +∞)
Заметим, что на этом промежутке, выражение под модулем х+2 всегда принимает положительные значения, в этом легко убедиться взяв любое число из рассматриваемого промежутка, например: х=0 и подставив в модуль: x+2=-0+2>0
Таким образом, на рассматриваемом промежутке: x+2>0→ |х+2|=x+2 в итоге на этом промежутке исходное уравнение после раскрытия модулей будет иметь вид:
х²+4х+1=2(х+2) → х²+2х-3=0 → х1=-3 и х2=1; проверкой убираем посторонний корень х1=-3, так как он не удовлетворяет условию х+2≥0
