Уравнения с модулями, методы решений. Часть 1.
Прежде чем приступать к непосредственному изучению техник решения таких уравнений, важно понять суть модуля, его геометрическое значение. Именно в понимании определения модуля и его геометрическом смысле, заложены основные методы решения таких уравнений. Так называемый, метод интервалов при раскрытии модульных скобок, настолько эффективен, что используя его возможно решить абсолютно любое уравнение или неравенство с модулями. В этой части мы подробно изучим два стандартных метода: метод интервалов и метод замены уравнения совокупностью.
Однако, как мы убедимся, эти методы, всегда эффективные, но не всегда удобные и могут приводить к долгим и даже не очень удобным вычислениям, которые естественно потребуют большего времени на их решение. Поэтому важно знать и те методы, которые решение определенных структур уравнений значительно упрощают. Возведение обеих частей уравнения в квадрат, метод введения новой переменной, графический метод, решение уравнений, содержащих модуль под знаком модуля. Эти методы мы рассмотрим в следующей части.
Определение модуля числа. Геометрический смысл модуля.
Первым делом познакомимся с геометрическим смыслом модуля:
Модулем числа а (|а|) называют расстояние на числовой прямой от начала координат (точки 0) до точки А(а).
Исходя из этого определения рассмотрим некоторые примеры:
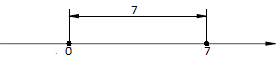
|7| - это расстояние от 0 до точки 7, конечно оно равно 7. → | 7 |=7
|-5|- это расстояние от 0 до точки -5 и оно равно: 5. → |-5| = 5

Все мы понимаем расстояние не может быть отрицательным! Поэтому |х| ≥ 0 всегда!
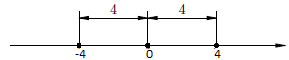
Решим уравнение: |х |=4
Это уравнение можно прочитать так: расстояние от точки 0 до точки x равно 4. Ага, получается, от 0 мы можем двигаться как влево так и вправо, значит двигаясь влево на расстояние равное 4 мы окажемся в точке: -4, а двигаясь вправо окажемся в точке: 4. Действительно, |-4 |=4 и |4 |=4.
Отсюда ответ х=±4.
При внимательном изучении предыдущего уравнения можно заметить, что: расстояние вправо по числовой прямой от 0 до точки равно самой точке, а расстояние влево от 0 до числа равно противоположному числу! Понимая, что вправо от 0 положительные числа, а влево от 0 отрицательные, сформулируем определения модуля числа: модулем (абсолютной величиной) числа х (|х|) называется само число х, если х ≥0, и число – х, если х <0.
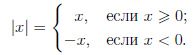
Прежде, чем идти дальше, рассмотрим неравенство и устно, ответьте на несколько заданий, которые помогут закрепить базовые знания, геометрическую интерпретацию и определение модуля.
|х | <3
Здесь нам надо найти множество точек на числовой прямой расстояние от 0 до которых будет меньше 3, давайте представим числовую прямую, на ней точка 0, идем влево и считаем один (-1), два (-2) и три (-3), стоп. Дальше пойдут точки, которые лежат дальше 3 или расстояние до которых от 0 больше чем 3, теперь идем вправо: один, два, три, опять стоп. Теперь выделяем все наши точки и получаем промежуток х:(-3;3).

Важно, чтобы вы это четко видели, если пока не получается, нарисуйте на бумаге и посмотрите, чтобы эта иллюстрация была вам полностью понятна, не поленитесь и попробуйте в уме увидеть решения следующих заданий:
|х |=11, х=? |х|=-5, х=?
|х | <8, х-? |х| <-6, х-?
|x |>2, х-? |x|> -3, х-?
|π-3|=? |-х²-10|=?
|√5-2|=? |2х-х²-3|=?
|х²+2|=? |х²+4|=0
|х²+3х+4|=? |-х²+9| ≤0
Обратили внимание на странные задания во втором столбце? Действительно, расстояние не может быть отрицательным поэтому: |х|=-5- не имеет решений, конечно же оно не может быть и меньше 0, поэтому: |х| <-6 тоже не имеет решений, ну и естественно, что любое расстояние будет больше отрицательного числа, значит решением |x|> -3 являются все числа.
После того как вы научитесь быстро видеть рисунки с решениями читайте дальше.






