Сначала рассмотрим простейшую задачу с однородными краевыми условиями первого типа.
Задача. На концах стержня конечной длины поддерживается нулевая температура. Источники тепла в стержне отсутствуют (однородное уравнение). Начальная температура в каждой точке стержня задана.
Решение. Функция 
– температура стержня – есть решение задачи:
(1)
Следуя методу Фурье, ищем сначала нетривиальные решения уравнения, удовлетворяющие однородным краевым условиям, в виде:
Знакомая схема приводит к соотношению:
.
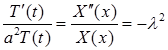Для задачи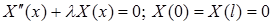 
известны собственные значения 
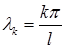и собственные функции 
Каждому собственному значению 
соответствует функция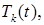 
удовлетворяющая уравнению первого порядка:
Общее решение этого уравнения имеет вид:
Значит, частные решения однородного уравнения теплопроводности, удовлетворяющие однородным граничным условиям, представляются в виде:
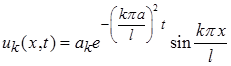
Здесь введена новая постоянная 
. Осталось просуммировать решения 
(2)
В заключительной части метода Фурье определяются постоянные 
так, чтобы функция (2) удовлетворяла заданному начальному условию
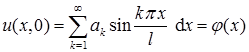(3)
Формула (3) показывает, что суть коэффициенты разложения начальной функции 
в ряд Фурье по синусам на 
, то есть
●
