РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Факультет «Управление процессами перевозок»
Контрольная работа
по дисциплине «Основы электродинамики направляющих систем»
Выполнил: студент 4 курса
Птушко Д. А.
Шифр 0812-АТС-1188
Москва 2013 г.
Задача №1
ЗАДАЧА 1
По стальному проводу [электрическая проводимость γ = 107 (Ом*м)-1; относительная магнитная проницаемость µ = 103] диаметром 2а = 6,04 мм течет синусоидальный ток І = 100 А частотой ƒ Гц.
Определить плотность тока на поверхности и на оси провода.
Вариант численного значения частоты тока определяется по формуле:
ƒ= 1,38866 • n2 Гц,
где n — последняя цифра шифра студента
Привести вывод формул для определения плотности тока δ и напряженности Н в любой точке сечения провода, не учитывая влияния обратного провода на поле в прямом проводе. При решении задачи использовать цилиндрическую систему координат.
Решение:
Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью γ и магнитной проницаемостью μ а
Обратимся к первому и второму уравнениям Максвелла, записанным в комплексной форме для синусоидально изменяющихся во времени Е и Н:
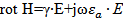
и
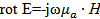
В проводящей среде даже при очень высоких частотах произведение ωεа много меньше проводимости γ. Поэтому с большой степенью точности слагаемым
jωεа Е в первом уравнении Максвелла для проводящих сред можно пренебречь.
Вектор плотности тока 
, записанный в комплексной форме для синусоидально изменяющихся во времени и тока І, удобно направить в положительном направлении оси z, поэтому = z0 .
Таким образом первое и второе уравнения Максвелла для проводящей среды приобретают вид:
=
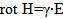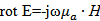
из первого уравнения Е·γ = .
Умножим обе части второго уравнения на γ0: 
· 
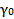
или,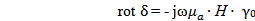 
,
Возьмем ротор от последнего уравнения:
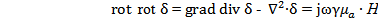
считая процесс течения тока установившимся, т.е. div σ = 0 и подставляя σ = z0·σ перейдем к скалярному уравнению
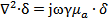
которое и требуется решить в цилиндрической системе координат. Учитывая вид оператора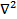 
= div grad, в этой системе координат, а также то, что σ от α и от z не зависит (из соображений симметрии), получим:
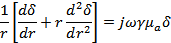
Введем обозначение q2= 
, тогда уравнение примет вид:
или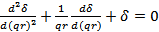 
Последнее уравнение является частным случаем уравнения Бесселя относительно аргумента х = qr и функции у = δ. Его решение имеет вид:
δ= А·J0 (qr) + ВN0 (qr),
где А и В — постоянные интегрирования;
J0 (qr) - функция Бесселя нулевого порядка первого рода;
N0 (qr) - функция Бесселя нулевого порядка второго рода.
Последняя обращается в бесконечность на оси провода, т.е. при r = 0, хотя из очевидных физических соображений ясно, что плотность тока должна быть всюду конечна, в том числе и на оси провода. Поэтому принимаем B = 0.
Следовательно, решение имеет вид:
δ= А·J0 (qr)
Используя второе уравнение Максвелла, определим напряженность магнитного поля:
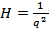rot δ= α0 
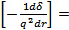α0 H
Определим постоянную интегрирования А, для чего только что полученное выражение для Н, взятое на поверхности провода (при r = а) приравняем к известному выражению для Я из закона полного тока:
А=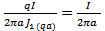 
Подставим найденное значение А в полученные выше решения для δ и Н:
; 
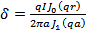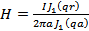
С помощью этих формул можно определить комплекс плотности тока δ и комплекс напряженности поля H в любой точке сечения провода. Радиус r может принимать значения от 0 до а. Для точек на оси провода r = 0; для точек на поверхности провода r = а.
Так как J0 (0) = 1, то плотность тока на оси провода:
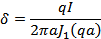
Введем это выражение в формулу решения: δ = δ0 J0 (qr).
Тогда плотность тока на поверхности провода: δ = δ0 J0 (qa).
Очевидно, что произведение qr есть комплексное число:
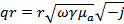
Бесселевы функции от комплексного аргумента также являются комплексными и могут быть представлены в показательной форме:
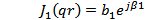
где b0 — модуль;
β0 — аргумент функции J0 (qr);
b1 — модуль;
β1 — аргумент функции J1(qr), которые определяются по значению 
помощью табл. 1.
При составлении этой таблицы наличие множителя 
в составе аргумента qrуже учтено.
