Реакции между кислотами и основаниями широко используются в анализе. На этих реакциях основан самый известный титриметрический метод – метод нейтрализации. Кислотность раствора, характеризуемая величиной рН, – важнейший фактор, влияющий на аналитические реакции любого типа. Например, на скорость и равновесие реакций комплексообразования и окисления-восстановления, на процессы осаждения, экстракции, ионного обмена. Влияние рН раствора особенно важно при разделении и опознании ионов с использованием качественных реакций (см. раздел 4.2), при комплексонометрическом титровании (раздел 4.5), в фотометрическом анализе – при переводе определяемого вещества в окрашенное соединение (раздел 6.3), при экстракционном концентрировании микропримесей (раздел 7.2). В этих и многих других случаях необходимо управлять кислотно-основными процессами в растворах и эффективно использовать их. Для разработки методик и осознанного проведения качественного и количественного анализа химик должен уметь:
· оценивать степень протекания кислотно-основной реакции по величине константы равновесия, с учетом концентрации реагентов;
· рассчитывать рН раствора заданного состава и, наоборот, подбирать состав раствора, обеспечивающий заданное значение рН;
· определять состояние растворенного вещества при разных рН (строить ионные диаграммы) и рассчитывать мольную долю любой формы этого вещества при заданном рН;
· подбирать значение рН, оптимальное для проведения какой-либо аналитической реакции, для перевода реагента в наиболее реакционноспособную форму.
Для решения всех этих задач нужна хорошо разработанная теория кислотно-основных процессов, пригодная как для водных, так и для неводных растворов.
Теории кислот и оснований. Представления о кислотно-основных свойствах веществ формировались постепенно, начиная со времен алхимии. В XVII–XIX веках начали складываться первые теории, связывающие кислотно-основные свойства веществ с их составом (Р. Бойль, А.Л. Лавуазье, Г. Дэви, Ж. Гей-Люссак, П. Дюлонг, И.Я. Берцелиус). В настоящее время используются:
· теория электролитической диссоциации (С. Аррениус, В. Оствальд),
· протолитическая теория (И. Бренстед, Т. Лоури),
· электронная теория (Г. Льюис).
Напомним, что, согласно теории электролитической диссоциации, кислотой называют вещество, которое при диссоциации в водном растворе из катионов образует только ионы Н+, основанием – вещество, которое при диссоциации из анионов образует только ионы ОН–. По протолитической теории кислота – это частица (молекула или ион), которая способна отдавать ион Н+ («протон»), основание – частица, принимающая протон. В электронной теории кислота – это акцептор электронной пары при образовании донорно-акцеп-
торной связи, а основание – донор электронной пары.
Естественно, реальные свойства вещества, его способность быть кислотой или основанием, не зависят от того, какую теорию мы выберем. Вещества классифицируют по объективным признакам. Так, к классу кислот относят вещества, определенным образом взаимодействующие с основаниями, металлами, спиртами; вызывающие появление характерной окраски цветных индикаторов и т. п. Любая теория должна согласовываться с фактами, поэтому вещество, проявляющее вышеперечисленные признаки, например СН3СООН в водном растворе, в рамках любой из названных теорий должно считаться кислотой. К сожалению, ни одну из известных теорий нельзя применить для прогнозирования кислотно-основных свойств всех веществ и для любых условий. Каждая теория имеет свои преимущества и ограничения.
Теория электролитической диссоциации, созданная еще в XIX веке и до сих пор используемая электрохимиками и школьными учителями, имеет хорошо разработанный математический аппарат. Но она рассматривает очень узкий круг кислот и оснований (только молекулы и ионные кристаллы типа NаОН). Она неприменима к неводным растворам и процессам, идущим в отсутствие растворителя. А в электронной теории Льюиса, часто используемой химиками-органи-
ками, не находят объяснения амфотерные свойства веществ. Теория Льюиса (как и более поздние теории Усановича и Пирсона) рассматривает кислотно-основные процессы слишком обобщенно. Эти теории не дают количественного описания кислотно-основных равновесий, что необходимо для разработки методик анализа.
В аналитической химии наибольшее признание получила протолитическая теория Бренстеда–Лоури. По этой теории кислотные или основные свойства характерны не только для молекул, но и для других частиц, в том числе для ионов. В результате кислотно-основ-
ные свойства самых разных веществ описываются одним и тем же способом[1]. Протолитическая теория позволяет легко рассчитывать кислотность неводных растворов и прогнозировать влияние растворителя. Недостатком этой теории является лишь невозможность объяснить с ее помощью кислотные свойства молекул, не содержащих атомов водорода.
Основные положения протолитической теории. Эта теория предложена практически одновременно (в 1923 г.) И. Бренстедом (Дания) и Т. Лоури (Великобритания), но в дальнейшем развивал ее именно Бренстед, поэтому нередко говорят: «теория Бренстеда». Основной постулат: проявление кислотных или основных свойств какого-либо вещества требует участия другого вещества, с противоположной функцией. Реакция между ними обязательно включает передачу протонов от кислоты к основанию. В результате реакции образуются новая кислота и новое основание. Такую реакцию называют протолитической. Ее участниками, как уже было сказано, могут быть любые частицы – молекулы и ионы.
Две частицы – кислота НА и основание А, отличающиеся по своему составу на один протон, образуют сопряженную протолитическую пару и могут в рамках теории Бренстеда рассматриваться как две формы одного и того же вещества. В ходе реакции кислотная форма одной сопряженной пары (НА) реагирует с основной формой (B) другой пары, при этом образуется основание А и кислота НВ. Общая схема протолитической реакции:
Например: СН3СООH + NH3 ÆСН3СОО– + NH4+ .
Протолитическое равновесие может быть смещено в ту или иную сторону при добавлении посторонних веществ, реагирующих с каким-либо из участников основной реакции. В частности, равновесие смещается при изменении рН раствора.
Частный случай протолитической реакции – протолиз, т. е. взаимодействие частиц растворенного вещества с растворителем. Особую роль в реакциях протолиза играют протоны. Эти заряженные частицы имеют ничтожно малые размеры, а потому обладают сильнейшим электрическим полем. Поэтому изолированный протон Н+ в растворе не существует. Как и другие растворенные частицы, он сольватируется растворителем, образуя ионы H3O+ в воде, СН3СООH2+ в безводной уксусной кислоте и т. д. Перенос протона от кислот к основаниям идет не только при прямом столкновении соответствующих частиц, но и по сложному «эстафетному» механизму, в котором участвуют молекулы растворителя (см. дополнительную литературу). Это объясняет высокую скорость кислотно-основных реакций в растворах.
Поскольку растворитель – активный участник протолитического процесса, от него зависят свойства растворенного вещества. Например, в водном растворе хлороводородная кислота ведет себя как сильная, т. е. полностью и необратимо протолизующаяся кислота:
HCl + H2O ® Cl– + H3O+ .
В среде растворителя, проявляющего кислотные свойства (протогенного), например, в среде ледяной уксусной кислоты, HCl ведет себя как слабая кислота.Протолиз идет обратимо,устанавливается равновесие:
HCl + СН3СООН ÆCl– + СН3СООH2+ .
Степень протекания этой реакции гораздо меньше единицы.
Таким образом, в рамках теории Бренстеда никакому веществу нельзя приписывать неизменных кислотно-основных характеристик; нельзя, например, считать, что соляная кислота всегда сильная, а уксусная – всегда слабая. Кислотно-основные свойства одного и того же вещества зависят от того, с чем оно реагирует, в каком растворителе это происходит. Можно сформулировать общее правило: чем сильнее выражены кислотные свойства растворителя, тем слабее проявляются в этом растворителе кислотные свойства растворенных веществ и сильнее – их основные свойства. Это правило позволяет целенаправленно регулировать свойства растворенного вещества, подбирая подходящий растворитель.
Если одним из компонентов протолитической пары является сильная кислота, то второй компонент пары не проявляет основных свойств, не влияет на рН раствора. Так, сильной (в водных растворах) кислоте НCl соответствует очень слабое основание – ион Cl–. Этот ион не вступает во взаимодействие с молекулами воды, не может «оторвать» от них протон. Значение рН водного раствора NaCl не зависит от концентрации хлор-ионов, оно определяется другим процессом (автопротолизом растворителя). Однако в безводной СН3СООН HCl – слабая кислота, в этой среде Cl– действительно является основанием, хотя и слабым.
Можно привести еще один пример. Такие водородсодержащие вещества, как метанол (СН3ОH) или аммиак (NH3), в водных растворах не проявляют кислотных свойств, не отдают протон молекулам воды. Зато их сопряженные формы – анионы метилата (СН3О–) или амида (NH2–) в водной среде являются очень сильными основаниями.
Приведенные примеры можно обобщить и сформулировать следующее общее правило: чем более сильной кислотой является одна из сопряженных форм, тем более слабым основанием будет в том же растворителе другая. И наоборот. Это правило позволяет делать прогнозы, полезные для обоснования соответствующих методик анализа. Так, известно, что в водном растворе и уксусная, и борная кислоты являются слабыми, но уксусная все же более сильная, чем борная. Сопряженные формы этих кислот – ацетаты и бораты – являются основаниями. С учетом выведенной закономерности, основные свойства ацетат-иона должны быть выражены намного слабее, чем у борат-иона. Действительно, ацетат-ионы в водном растворе не удается оттитровать какой-либо сильной кислотой, а соли борной кислоты (например, бура) прекрасно титруются.
Протолитические свойства растворителей. Автопротолиз. Шкала рН. По протолитическим свойствам растворители делят на несколько групп:
· апротонные, не содержащие подвижных протонов, малополярные (с очень низкой величиной диэлектрической проницаемости e) и не способные к участию в протолитических реакциях. К их числу относятся углеводороды и их галогенпроизводные, например, С6Н6, СCl4, а также CS2 и др.;
· протогенные (кислотные), легко отдающие протоны, но способные и к их присоединению (безводные СН3СООH, НСООH и другие вещества);
· протофильные (основные), легко присоединяющие протоны, но способные и к их отдаче (этилендиамин H2N(СН2)2NH2 и другие амины, амиды, гидразин, жидкий аммиак);
· амфипротные, в равной степени способные присоединять и отдавать протоны (спирты).
Иногда выделяет и другие группы растворителей, в частности:
· протоноакцепторные, способные только к присоединению протонов (пиридин С5Н5N);
· диполярные апротонные (ДАР) – более полярные (e > 15), чем другие апротонные растворители. Их кислотно-основные свойства слабо выражены. Примеры: ацетон (СН3)2СО, диметилформамид (СН3)2NСНО, диметилсульфоксид (СН3)2SО, ацетонитрил СН3СN.
В среде растворителей, обладающих протолитическими свойствами (протогенных, протофильных и амфипротных), а также в некоторых диполярных апротонных растворителях происходит автопротолиз – перенос протонов от одних молекул растворителя HL к другим. Схематически процесс автопротолиза можно представить так:
HL + HL ÆH2L+ + L–.
Образующиеся при этом собственные ионы растворителя получили особые названия – лионий (H2L+) и лиат (L–). Равновесие характеризует константа автопротолиза К HL, постоянная для данного растворителя при данной температуре величина:
К HL = a H2L+ a L– ≈ [H2L+] [L–]. (3.13)
Переход от активностей к концентрациям связан с тем, что в малополярных неводных растворителях коэффициенты активности ионов можно считать равными единице. В справочной литературе приводятся обычно не сами константы автопротолиза, а их показатели (табл. 3.2). Здесь и далее оператор р (показатель) обозначает взятие десятичного логарифма и изменение его знака на противоположный. Так, pH = – lg [H+], рК = – lgK, р К HL= –lg К HL.
Таблица 3.2
Свойства некоторых растворителей
| Растворитель | Формула | р К HL | e | Тип растворителя |
| Вода | Н2О | 14,0 | Амфипротный | |
| Этанол | С2Н5OH | 19,0 | 24,3 | Амфипротный |
| Бутанол (третичный) | (СН3)3СOH | 24,5 | 10,9 | Амфипротный |
| Уксусная кислота (безв.) | СН3СООH | 14,4 | 6,2 | Протогенный |
| Этилендиамин | H2N(СН2)2NH2 | 15,3 | 12,5 | Протофильный |
| Ацетонитрил | СН3СN | 33,3 | 38,0 | ДАР |
Процесс автопротолиза, идущий в водных растворах по уравнению
H2O + H2O ÆH3O+ + ОН– ,
описывает ионное произведение воды Кw = a H3O+ a OH–= 1,0 ∙10–14, р Кw = 14,00 (при 25°С). Коэффициенты активности ионов гидроксония и гидроксила могут существенно отличаться от единицы; это надо учитывать при значительной ионной силе раствора. Однако в большинстве случаев высокая точность расчетов не требуется, и при описании кислотно-основных процесссов принимают:
Кw = [H3O+][OH–]. (3.14)
Кислотность растворов принято описывать с помощью введенного С. Серенсеном водородного показателя (рН). Для водной среды
рН = – lg a H3O+. (3.15)
Часто принимают, что a H3O+≈ [H3O+], и рассчитывают рН водного раствора по приближенной формуле: рН = – lg [H3O+]. Для произвольного протолитического растворителя определяют рН раствора по обобщенной формуле:
рН = – lg [H2L+]. (3.16)
Величину рН раствора можно определить опытным путем, обычно используют потенциометрический метод (разд. 6.1.2). Однако, зная состав раствора, его рН можно предвидеть. Проще всего рассчитать рН растворов сильных кислот и оснований, сложнее – растворов слабых протолитов, еще труднее – pH смеси нескольких протолитов разной силы.
Характер среды (кислая, щелочная или нейтральная) определяется соотношением между равновесными концентрациями лиония и лиата. В кислой среде концентрация лиония выше, чем концентрация лиата; в щелочной, наоборот, концентрация лиата выше, чем концентрация лиония; в нейтральной среде эти концентрации равны.
В чистом растворителе и в растворах веществ, не обладающих протолитическими свойствами, [H2L+] = [L–] = 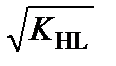 . После логарифмирования получаем: рН = р К HL / 2. Это выражение характеризует нейтральную среду, независимо от природы растворителя. В нейтральном водном растворе [H3O+] = [OH–] =
. После логарифмирования получаем: рН = р К HL / 2. Это выражение характеризует нейтральную среду, независимо от природы растворителя. В нейтральном водном растворе [H3O+] = [OH–] = 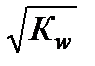 = 1,0 ∙10–7 моль/л, откуда рН = pKw2= 7,00 (при 298 К). В растворахкислот в результате протолиза повышается концентрация ионов лиония (для водных растворов – гидроксония). В этом случае [H2L+] >
= 1,0 ∙10–7 моль/л, откуда рН = pKw2= 7,00 (при 298 К). В растворахкислот в результате протолиза повышается концентрация ионов лиония (для водных растворов – гидроксония). В этом случае [H2L+] >  , а рН < р К HL/2. В водных растворах кислот [H3O+] >
, а рН < р К HL/2. В водных растворах кислот [H3O+] >  и рН < 7. В растворахоснований, напротив, рH > р К HL/2, в частности, в водных растворах оснований рН > 7.
и рН < 7. В растворахоснований, напротив, рH > р К HL/2, в частности, в водных растворах оснований рН > 7.
Границами шкалы рН в любом протолитическом растворителе считают значения рН, соответствующие 1 М растворам лиония и лиата, т. е. рН, равные 0 и р К HL. В частности, при 298 К в водных растворах 1 М раствор сильной кислоты дает (без учета ионной силы) рН = 0, а 1 М раствор сильного основания рН = 14.
Рис. 3.3. Шкала рН в воде (а)
и в произвольном протолитическом растворителе (б)
При повышении температуры автопротолиз усиливается, К HL растет, поэтому границы шкалы и точка нейтральности смещаются. Так, при 100 °С р Кw = 12,26, поэтому рН нейтрального водного раствора при этой температуре равен не 7,00, а 6,13.
Одно и то же числовое значение рН в разных растворителях может соответствовать разным средам. Так, рН = 9,5 в водном растворе – это слабощелочная среда, но в среде этанола (р К HL = 19) – это нейтральная среда, а в среде бутанола (р К HL = 24,5) – кислая. Стоит обратить внимание, что шкала рН для большинства неводных протолитических растворителей длиннее, чем в случае водных растворов. Это способствует раздельному титрованию нескольких кислот (или нескольких оснований) в неводных растворах.
Расчет рН растворов сильных протолитов. Введем следующие допущения:
· в растворе содержится только одно вещество, способное к протолизу;
· частица такого вещества присоединяет или отдает только один протон;
· протолиз идет необратимо и количественно (на 100 %);
· влиянием ионной силы раствора можно пренебречь;
· концентрация протолита достаточно высока по сравнению с концентрацией продуктов автопротолиза. Этому условию соответствуют водные растворы, если С > 10–5 М.
При выполнении всех перечисленных условий по исходной (аналитической) молярной концентрации растворенного вещества С сразу можно найти концентрацию ионов H3O+ или ОН–. А именно, в водном растворе сильной кислоты [H3O+] = С кисл,
рН = –lg С кисл = р С кисл. (3.17)
В водном растворе сильного основания (NаОН или СН3ОNа) [OH–] = С осн
[H3O+] =  =
= 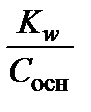 =
= 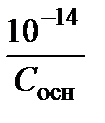 , рН = 14 – р С осн. (3.18)
, рН = 14 – р С осн. (3.18)
Для вычисления рН неводного раствора сильного основания в формулу (3.18) надо подставить соответствующее значение константы автопротолиза:
рН = р К HL– р С осн. (3.19)
Пример 3.1. Рассчитать рН 5·10–3 М водного раствора КОН.
Решение. Величина рН этого раствора определяется присутствием сильного основания – ионов ОН–, катион К+ не проявляет протолитических свойств. Используем формулу (3.18):
рН = 14 + lg(5·10–3) = 11,7.
При выводе уравнений (3.17–3.19) не были учтены концентрации ионов H3O+ и ОН–, образующихся при автопротолизе воды. Поэтому при очень низкой (< 10–5 М) концентрации сильного протолита эти формулы неприменимы. Так, формула (3.17) привела бы к тому, что 10–9 М водный раствор HCl оказался бы имеющим рН = 9, т. е. щелочным! Для точных расчетов рН, особенно в растворах с достаточно высокой ионной силой, следует находить рН по уравнению (3.15) с учетом коэффициента активности иона H3O+. При расчете рН двупротонных сильных кислот и оснований (H2SO4, Ва(ОН)2 и др.) следует учитывать стехиометрию реакции протолиза и соответственно преобразовать расчетные формулы.
Константы равновесия протолитических реакций. Применим закон действия масс (в его концентрационной форме) к процессу протолиза слабой однопротонной кислоты HА в водном растворе:
HА + H2O ÆА + H3O+;
Kа =  . (3.20)
. (3.20)
Поскольку слабая кислота HА и сопряженное с ней основание А могут быть нейтральными молекулами, катионами или анионами, то заряды таких частиц в обобщенных схемах протолиза опускают. Концентрационную константу равновесия (3.20) называют константой кислотности, кислотной константой или константой кислотной ионизации. Она характеризует не какую-либо отдельную частицу (например, НА), а сопряженную пару НА/А. При переходе к другому растворителю или другой температуре значение К а для данной пары изменится. Экспериментально измеренные при 20–25 °С константы кислотности приводятся в справочниках. Как правило, там указаны не сами константы, а их показатели. Величина К а зависит и от ионной силы раствора, но это влияние – довольно слабое, и на практике им пренебрегают, подставляя в соответствующие формулы значения p Ка, взятые прямо из справочной литературы, без поправок на ионную силу данного раствора.
Величина К а тем выше, а р Ка тем меньше, чем сильнее протолизуется кислота. Наиболее сильной кислотой в водном растворе является ион гидроксония, для него условно принимают Ка = 1 и р Ка = 0. Уксусная кислота (ее формулу можно записать в виде HAc) характеризуется величиной p Ka = 4,76, катион аммония имеет p Ka = 9,24 и т. д. Для сильных кислот величина Kа не определяется.
В водном растворе слабого однопротонного основания А протолиз идет по схеме А + H2O ÆНА + OH–. Силу такого основания характеризует константа основности Kb:
Kb = 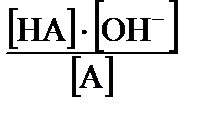 . (3.21)
. (3.21)
Чем сильнее основание, тем выше его Kb и ниже р Kb. Самое сильное основание, существующее в водном растворе, – это гидроксид-ион, для которого условно принимают Kb = 1 и р Kb = 0.
Константы кислотности и основности сопряженных протолитов связаны; в этом можно убедиться, перемножив уравнения (3.20) и (3.21). Для водных растворов получим:
Kа Kb = Кw р Kа + р Kb = 14. (3.22)
Аналогично, для произвольного растворителя получаем:
Kа Kb = К HL р Kа + р Kb = р К HL.(3.22а)
Поэтому величину р Kа можно использовать как характеристику протолитической пары в целом: чем выше р Kа, тем слабее кислота и тем сильнее сопряженное основание (рис. 3.4):
Рис. 3.4. Сила кислот и оснований в водном растворе
в зависимости от величины рKа сопряженных протолитических пар
На основании уравнений (3.22) и (3.23) в случае необходимости оценивают свойства одного из сопряженных протолитов, если в справочнике есть данные для другого. К сожалению, в справочниках нередко можно найти данные только для молекулярных протолитов. А ведь многие ионы тоже обладают кислотными или основными свойствами. В частности, катионы металлов, кроме щелочных и щелочноземельных, являются слабыми кислотами. Это происходит благодаря воздействию катиона на молекулы воды, содержащиеся в гидратной оболочке. Например:
[Al(H2O)6]3+ + H2O Æ[AlOH(H2O)5]2+ + H3O+
(или Al3+ + H2O Æ[AlOH]2+ + Н3O+) .
Продукты протолиза таких кислот – гидроксокомплексы соответствующего металла. Входящие в состав комплекса молекулы воды при записи обычно опускают.
Протолиз многопротонных слабых кислот и оснований протекает ступенчато, в каждом из этих процессов происходит перенос только одного протона. Равновесие каждой ступени протолиза характеризуется своим значением Kаi или Kbi, причем наиболее сильно протолиз идет по первой ступени. Для многопротонных кислот характерно, что Kа 1 > Kа 2 > Kа 3, а для оснований – Kb 1 > Kb 2 > Kb 3.
Протолиз катиона [Al(H2O)6]3+ на первой стадии идет примерно в той же степени, что и протолиз молекул уксусной кислоты, но на второй стадии лишь немногие частицы гидроксокомплекса алюминия отдают основаниям еще один протон:
[AlOH(H2O)5]2+ + H2O Æ[Al(OH)2(H2O)4]+ + H3O+ .
Теоретически процесс протолиза может дойти и до [Al(OH)6]3–.
Если в растворе, помимо растворителя, содержатся кислота и основание разных протолитичесих пар, между ними возможна химическая реакция. Полноту протекания такой реакции можно оценить по ее константе равновесия. Рассмотрим реакцию, идущую по схеме:
HA + B ÆA + HB.
Растворитель в этой реакции непосредственно не участвует. Константа равновесия равна:
Кравн =  .
.
Предположим, процесс взаимодействия проходит в водном растворе. Выпишем константы кислотности обеих протолитических пар (см. уравнение 3.20).
Кa 1=  [H3O+]; Кa 2=
[H3O+]; Кa 2=  [H3O+].
[H3O+].
Если разделить эти константы друг на друга, получится константа равновесия:
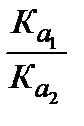 =
= 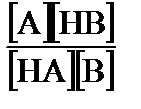 = Кравн.
= Кравн.
После логарифмирования получаем важную расчетную формулу:
lg Кравн = p Ka 2– p Ka 1. (3.23)
Таким образом, величина константы равновесия реакции между основанием и кислотой (реакции нейтрализации) определяется разностью р Ка протолитических пар, к которым принадлежат эти вещества.
Пример 3.2. Рассчитать константу равновесия для реакции между уксусной кислотой и аммиаком в водном растворе:
СН3СООН + NH3 ÆСН3СОО– + NH4+ .
Решение. Найдем в справочной литературе значения показателей кислотных констант: для системы уксусная кислота/ацетат-ион в водном растворе рКа1 = 4,76; для системы ион аммония/аммиак рКа2, = 9,25. Константу равновесия рассчитываем по (3.23):
lg Кравн = 9,25 – 4,76 = 4,49, Кравн = 104,49.
Константа равновесия сравнительно невелика и не обеспечивает количественного протекания этой реакции. Именно поэтому реакцию (а также аналогичные ей) нельзя использовать в анализе.
Взаимодействие между двумя слабыми протолитами может характеризоваться еще меньшими константами равновесия. Так, в водном растворе реакция
НS– + NH3 ÆS2– + NH4+
характеризуется константой равновесия, равной 10–3,35. Судя по величине К равн , эта реакция в растворе практически не идет.
Расчет рН растворов слабых протолитов. Степень протекания реакции протолиза в растворе заданного состава называют степенью протолиза. Обозначим ее величину символом a t [2]. Пусть протолизу подвергается слабая кислота НА, продукт реакции – А. Тогда:
a t = 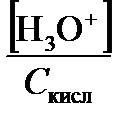 =
= 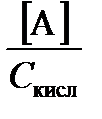 . (3.24)
. (3.24)
Если же протолизу подвергается слабое основание,
a t = 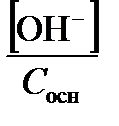 =
= 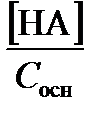 . (3.25)
. (3.25)
Константа равновесия и степень протолиза связаны друг с другом соотношением, которое называют законом разбавления Оствальда. Выведем это уравнение на примере слабой кислоты, учитывая, помимо уравнения (3.21), условие материального баланса:
С кисл = [НА] + [А]
Kа =  =
= 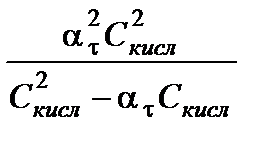 =
=  . (3.26)
. (3.26)
Для очень слабого протолита (a t. <<1) формула (3.26) упрощается до Kа =  . В таких случаях степень протолиза приблизительно равна:
. В таких случаях степень протолиза приблизительно равна:
a t=  . (3.27)
. (3.27)
Аналогичным образом для протолиза слабых оснований получаем:
a t= 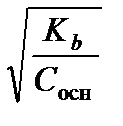 . (3.28)
. (3.28)
В любом случае протолиз слабых протолитов усиливается при разбавлении. Это приводит к изменению рН раствора.
Приближенную формулу для расчета рН раствора слабой кислоты можно вывести, комбинируя уравнения (3.24) и (3.27):
[H3O+] = a t С кисл = 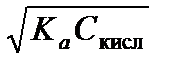 ,
,
откуда рН = 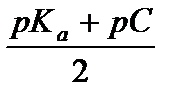 . (3.29)
. (3.29)
Аналогично для водного раствора слабого основания из уравнений (3.25) и (3.28) получаем:
[OH–] = a t С осн = 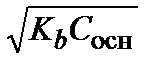
рН = p Кw – рОН = 14– 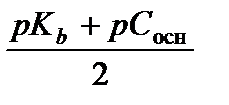 . (3.30).
. (3.30).
Выведенные формулы применимы далеко не во всех случаях. Легко доказать, что упрощение, сделанное при выводе формулы (3.27) и вытекающих из нее уравнений (3.29) и (3.30), приведет к значительной ошибке при расчете рН, если не выполняются условия:
С кисл > 102 Kа , С осн > 102 Kb . (3.31)
Кроме того, точный расчет должен учитывать концентрации ионов H3O+ и ОН–, образовавшихся при автопротолизе воды.
Пример 3.3. Рассчитать рН двух водных растворов – 0,10 М раствора муравьиной кислоты НСООН и 0,10 М раствора AlCl3.
Решение. Одноосновная муравьиная кислота в водном растворе является слабой (р Kа = 3,75). В таких случаях расчет pH следует вести по формуле (3.29). Однако надо проверить, выполняется ли условие (3.31). В данном случае оно выполняется, поэтому рН раствора равен 0,5 (3,75 + 1,0) = 2,38. Влиянием автопротолиза можно пренебречь, так как, судя по найденной величине рН, протолиз муравьиной кислоты дает гораздо больше ионов H3O+, чем автопротолиз растворителя.
По теории Бренстеда, катион алюминия – такая же слабая кислота, как уксусная или муравьиная. Рассчитывая рН раствора, содержащего гидратированные катионы алюминия по формуле (3.29), будем учитывать только первую ступень протолиза. Величина р Ка 1 = 3,0, которую можно найти для иона Al3+ в некоторых справочниках, соответствует условию (3.31). Следовательно, рН раствора равен 0,5 (3,0 + 1,0) ≈ 2,0. На самом деле раствор AlCl3 будет еще более кислым, так как протолиз идет не только по первой ступени.
Отметим, что, если константы протолиза катионных кислот типа иона алюминия не удается найти в справочной литературе, их можно вычислить по известным константам устойчивости гидроксокомплексов соответствующего металла.
Растворы многопротонных протолитов, амфолитов и смесей протолитов. Значения рН растворов многопротонных кислот и оснований можно рассчитать по ранее выведенным формулам (3.29) и (3.30), учитывая протолиз только по первой ступени (см. пример 3.3). Но такой расчет дает достаточно точные результаты только в том случае, если
р Kа 1< р Kа 2– 3 (для кислот) (3.32)
р Kb 1< р Kb 2– 3 (для оснований) (3.33)
При невыполнении этих условий решение получают на основе уравнений ЗДМ и материального баланса (см. дополнительную литературу). Расчет довольно сложен и обычно выполняется с помощью компьютера.
Пример 3.4. Рассчитать рН 0,010 М водного раствора Na2S.
Решение. Величина рН раствора определяется присутствием слабого двупротонного основания – иона S2– (р С = 2). Эти ионы способны к ступенчатому протолизу:
S2– + H2O ÆНS– + ОН– (1 ступень)
НS– + H2O ÆН2S + ОН– (2 ступень)
Рассчитаем константы основности:
р Kb (S2–) = 14,00 – р Kа 2(Н2S) = 14,00 – 12,60 = 1,40
р Kb (НS–) = 14,00 – р Kа 1(Н2S) = 14,00 – 7,00 = 7,00.
Показатели ступенчатых констант различаются более чем на 3 единицы, т. е. условие (3.33) выполняется. Для расчета рН достаточно учесть лишь первую ступень протолиза, для которой Kb = 0,040. Если рассчитывать рН раствора по формуле (3.30), будет получено значение рН = 12,3. Следовательно, автопротолиз можно не учитывать, протолиз сульфид-ионов дает гораздо больше ионов ОН, чем автопротолиз воды. Но формула (3.30) в данном случае даст большую погрешность, поскольку сульфид-ион нельзя считать очень слабым основанием, условие (3.31) здесь не соблюдается. Решение найдем преобразованием выражения для основной константы (3.21) с учетом уравнения материального баланса и равенства [OН–] = [НS–]:
Kb (S2–) = 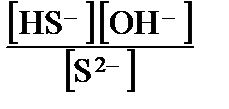 =
= 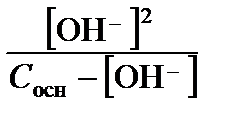 .
.
Получаем квадратное уравнение относительно [OН–]:
[OН–]2 + Kb [OН–] – KbС осн = 0.
Положительный корень этого уравнения:
[OН–] =  =
= 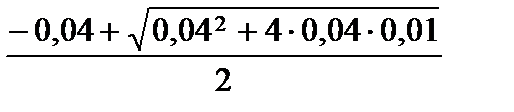 = 8,3∙10–3 моль/л.
= 8,3∙10–3 моль/л.
рН = 14 + lg(8,3∙10–3) = 11,92.
Заметим, что по формуле (3.31) мы получили бы значение рН = 12,3, отвечающее нереальной для данного раствора концентрации [OН–] = 0,02 моль/л.
Применение специального программного обеспечения позволило бы найти точное решение: величина рН данного раствора равна 11,92.
Аминокислоты, кислые соли и некоторые другие вещества являются амфолитами. Протолиз этих веществ идет одновременно по кислотному и основному типу. Так, в растворе кислой соли МНА анион НА– участвует сразу в двух реакциях:
НА– + H2O ÆН2А + OH–
НА– + H2O ÆА2– + H3O+.
Составляя уравнение электронейтральности и уравнение материального баланса, а затем проводя алгебраические преобразования на основе ЗДМ, можно получить приближенную формулу для расчета рН, справедливую лишь при достаточно высокой концентрации соли:
[H3O+] = 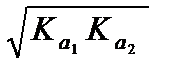 , (3.34)
, (3.34)
 . (3.35)
. (3.35)
Здесь р Ка 1, р Ка 2– показатели кислотных констант для сопряженных пар H2A/HA и HA/A, численно равные показателям ступенчатых констант диссоциации многопротонной кислоты, от которой происходит рассматриваемый амфолит. Из (3.35) следует, что рН раствора амфолита не зависит от его концентрации (во всяком случае, в первом приближении). Это подтверждает эксперимент. Водный раствор гидрокарбоната натрия имеет рН 8,34, что соответствует полусумме показателей кислотных констант угольной кислоты (р Ка 1 = 6,35, р Ка 2 = 10,32).
Формулу (3.35) можно использовать и для расчета рН раствора соли, состоящей из катионной кислоты и анионного основания, например, СН3СООNH4, NH4NO2 и т. п. В этом случае в формулу подставляют значения р Kа протолитических пар, к которым принадлежат катион и анион соли.
Пример 3.5. Рассчитать рН 0,1 М водного раствора NH4NO2 .
Решение. В растворе одновременно находятся слабая катионная кислота NH4+ и слабое анионное основание NO2–. Значит, растворенное вещество – амфолит, расчет рН ведут по формуле (3.35). Значения констант кислотности: р Kа (HNO2) = 3,16; р Kа (NH4+) = 14,00 – р Kb (NH3) = 14,00 – 4,76 = 9,24. Подстановка в (3.35) дает рН = 0,5 (р Ка 1+ р Ка 2) = 0,5∙(3,16 + 9,24) = 6,20.
Если в растворе присутствует несколько протолитов одинаковой природы, то рассчитать рН такого раствора довольно сложно, так как степень протолиза каждого компонента смеси зависит от природы и концентрации других компонентов. Придется учитывать целый ряд равновесий, составлять и решать систему уравнений. Однако в некоторых случаях расчет существенно упрощается. А именно, если:
· раствор содержит несколько сильных кислот или несколько сильных оснований. Концентрации ионов H3O+ (или ОН–) можно найти суммированием концентраций компонентов смеси. Величина рН смеси сильных кислот определяется по очевидной формуле:
рН = – lg 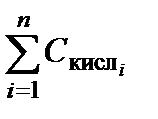 . (3.36)
. (3.36)
Величину рН смеси сильных оснований находят аналогичным образом:
рН = 14 + lg 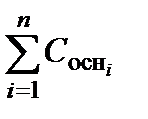 . (3.37)
. (3.37)
· раствор содержит сильную и слабую кислоты или сильное и слабое основания в приблизительно равных концентрациях. Поскольку сильный протолит подавляет протолиз слабого (сдвиг равновесия в соответствии с принципом Ле-Шателье), величину рН рассчитывают без учета присутствия слабого протолита.
Пример 3.6. Рассчитать рН водного раствора, 0,01 М по HCl и 0,05 М по НNO3 .
Решение. Раствор содержит смесь двух сильных кислот. Очевидно, [H3O+] = 0,01 + 0,05 = 0,06 моль/л. pH = – lg 0,06 = 1,2.
Ионные диаграммы и их интерпретация. В результате протекания кислотно-основных реакций в растворе любого слабого протолита одновременно существует несколько разных форм растворенного вещества. Состав таких растворов удобно представлять с помощью ионных (распределительных) диаграмм, показывающих, как меняется мольная доля отдельных форм растворенного вещества при изменении рН. В данном случае речь идет о молекулах и ионах, различающихся по степени протонированности. Так, в растворе однопротонного протолита – аммиака – присутствуют две формы: кислотная NH4+ и основная NH3. В растворе двухосновной сероводородной кислоты присутствуют три формы: молекулы H2S, однозарядные анионы HS– и двухзарядные анионы S2–. А в растворе трехосновной орто-фосфорной кислоты, как и в растворе любой соли этой кислоты, присутствуют четыре подобных формы.
Для построения ионных диаграмм нужно связать мольную долю каждой формы с величиной рН. Соответствующие расчетные формулы выводят из уравнений ЗДМ и условия материального баланса. Вначале рассмотрим раствор однопротонного протолита с общей концентрацией С (моль/л), в котором присутствуют два вида частиц – слабая кислота НА и ее сопряженное основание А. Выпишем выражение для константы кислотности (3.20) и преобразуем его.
Kа = 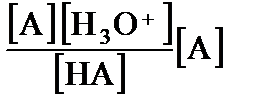 =
= 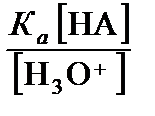 .
.
По определению, мольная доля кислотной формы равна a НА = 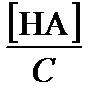 , основной – a А =
, основной – a А = 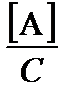 . Запишем уравнение материального баланса: С = [A] + [HA]. Проведем необходимые подстановки:
. Запишем уравнение материального баланса: С = [A] + [HA]. Проведем необходимые подстановки:
a НА =  =
=  =
= 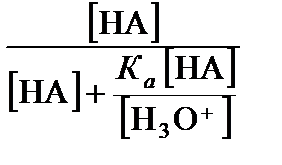 =
= 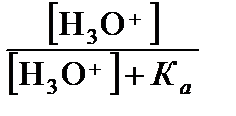 ,
,
a А = 1 – a НА = 1 –  =
= 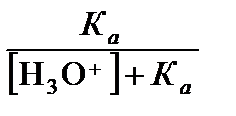 . (3.38)
. (3.38)
Аналогичным образом могут быть выведены формулы для описания более сложных случаев (сосуществование 3 или более сопряженных форм растворенного вещества). Так, состояние двухосновной кислоты (например, сероводорода) описывается следующим образом:
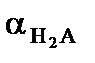 =
= 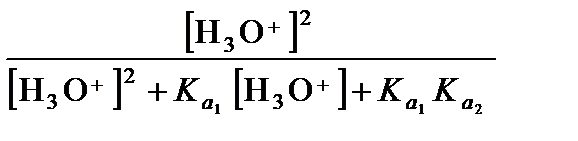 ,
,
a НА = 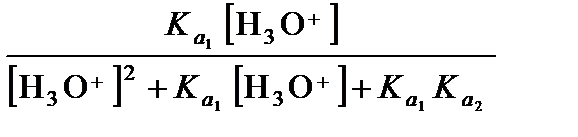 , (3.39)
, (3.39)
a А =  .
.
Ионные (распределительные) диаграммы для растворов слабых протолитов строят в координатах ai – рН (рис. 3.1, 3.5). Точное построение таких диаграмм возможно при компьютерном расчете мольных долей каждой формы при изменении рН с заданным шагом. Но общий вид ионной диаграммы, особенно для сравнительно простых систем с 2–3 сопряженными формами, можно представить и без такого расчета. Рассмотрим однопротонную систему, например, водный раствор аммиака. Из уравнения (3.38) следует, что в сильнокислой среде, где [H+] >> Ka a НА ≈ 1, а a А ≈ 0. А в сильнощелочной области, где [H+] << Ka, мольныедоли составляют: a А ≈ 1, a HA ≈ 0. Следовательно, при малых рН в растворе доминирует кислотная форма. Кривая, описывающая поведение этой формы, при рН << р Kа идет горизонтально на уровне a НА ≈ 1. Кривая начинает снижаться лишь за 1–2 единицы до рН = р Ка. Когда же величина рН станет на 1–2 единицы больше, чем р Ка, эта кривая вновь выйдет на горизонталь, но теперь она пойдет по оси абсцисс (a НА ≈ 0).
Рис. 3.5. Ионная диаграмма водного раствора аммиака (pKa = 9,24)
Вторая кривая, описывающая поведение основной формы, идет симметрично первой (рис. 3.5). Из уравнений (3.38) и (3.39) следует, что при рН = р Kа мольные доли обеих форм равны, каждая из них равна 0,5. Следовательно, обе кривые должны пересекаться в точке с абсциссой рН = р Kа и ординатой a = 0,5.
Для многопротонного протолита таким же образом строится участок диаграммы вблизи каждого значения рН = р Kаi, описывающего равновесие между двумя сопряженными формами.
Построение ионных диаграмм позволяет понять, что наиболее протонированная форма растворенного вещества доминирует в растворе при рН < p Kа 1; следующая – при рН от р Ка 1до р Ка 2и так далее. Наименее протонированная форма А доминирует при рН, превышающем показатель последней константы. Для «промежуточной» по своей протонированности формы растворенного вещества кривая на ионной диаграмме проходит через максимум. Он находится при рН, приблизительно равном полусумме показателей констант, характеризующих переходы промежуточной формы в более протонированную и менее протонированную. Отметим, что ионная диаграмма, описывающая равновесия протолиза, сохранит свой вид при изменении общей концентрации растворенного вещества.
Пример 3.7. Определить, в каком интервале значений рН в растворе пирофосфорной кислоты (H4P2O7) будут доминировать ионы HP2O73–.
Решение. Обозначим эту кислоту формулой H4R и найдем в справочниках значения показателей констант кислотности (они совпадают с показателями констант диссоциации). В данном случае р Ка 1 = 0,91; р Ка 2 = 2,10; р Ка 3 = 6,70; р Ка 4 = 9,32. Очевидно, в сильнокислой среде, вплоть до рН 0,91, доминируют молекулы H4R, в зоне рН от 0,91 до 2,10 – анионы H3R–, в зоне рН от 2,10 до 6,70 – ионы H2R2–, в зоне рН от 6,70 до 9,32 – те самые ионы HR3–, о которых идет речь в условии задачи, а в сильнощелочной области при рН > 9,32 доминируют полностью депротонированные ионы R4– . Максимальное значение мольной доли гидропирофосфат-анионов будет наблюдаться в середине их зоны доминирования, т. е. при рН = 0,5 ∙ (6,70 + 9,32) = 8,01. Именно это значение рН надо создать в растворе, чтобы перевести любые пирофосфаты, независимо от их начальной протонированности, в форму НР2О73–-ионов. Для решения данной задачи построение ионной диаграммы с помощью соответствующей компьютерной программы не обязательно, но оно подтверждает сделанный вывод (рис. 3.6). Видно, что максимальное содержание ионов HR3– в растворе (при рН 8) составляет около 90 %, т. е. полностью перевести пирофосфорную кислоту в эту форму нельзя.
Рис. 3.6. Состояние пирофосфорной кислоты в водном растворе:
1 – H4R; 2 – H3R– ; 3 – H2R2–; 4 – HR3–; 5 – R4–
Буферные растворы. Такие растворы используют для создания и поддержания необходимого значения рН, не меняющегося при разбавлении раствора и добавлении небольших количеств кислот и оснований. Буферными свойствами не обладают ни чистая вода, ни растворы сильных протолитов (кроме растворов очень высокой концентрации). Так, если к 1 л воды с рН = 7 добавить всего 10–4 моль сильной кислоты, рН раствора составит 4, т. е. изменится на 3 единицы. А если в 10–4 М раствор сильной кислоты ввести 10–3 моль сильного основания, то его рН возрастет примерно до 11.
Буферным называют раствор, который содержит слабую кислоту и ее сопряженное основание, причем их концентрации отличаются не более чем в 10 раз. К числу важнейших, наиболее часто используемых буферных систем, относятся ацетатная (СН3СООН, СН3СОО–), аммиачная (NH3, NH4+), фосфатная (H2PO4–, HPO42–) и др. Для приготовления буферных растворов берут хорошо растворимые, доступные реактивы: слабые кислоты и их соли, слабые основания и их соли, смеси солей многопротонных кислот. Некоторые соли обладают буферным действием и в «индивидуальном» растворе: в ходе протолиза они образуют пару сопряженных протолитов либо изначально содержат ион-амфолит. Примером солей первого типа является тетраборат натрия (бура) Na2B4O7 ·10Н2О. В ее водном растворе идет реакция:
В4О72– + 3Н2О = 2 Н3ВО3 + 2ВО2–.
Примером солей второго типа может быть гидрокарбонат натрия или гидротартрат калия (кислая соль винной кислоты).
Буферные растворы в лаборатории часто готовят путем неполной нейтрализации раствора слабого протолита рассчитанным количеством сильного протолита.
Необходимо уметь подбирать состав буферного раствора, обеспечивающего требуемое для проведения аналитической реакции значение рН, а также рассчитывать рН буферных растворов и предвидеть изменение их рН при добавлении протолитов.
Уравнение для рН буферного раствора легко вывести из выражения (3.20) путем его логарифмирования:
[H3O+] = Kа  ; рН = р Kа + lg
; рН = р Kа + lg  .
.
Присутствие в растворе второго компонента сопряженной протолитической пары подавляет протолиз данного протолита, поэтому без большой погрешности можно приравнять равновесные концентрации слабых кислоты и основания в буферном растворе их аналитическим концентрациям, считая, что [HA] ≈ C кисл, [A] ≈ C осн. Тогда можно записать:
рН = р Kа + lg  . (3.40)
. (3.40)
Полученное уравнение (3.40) (уравнение Гендерсона – Хас-
сельбаха) очень широко применяется химиками, причем не только аналитиками. Оно показывает, какие значения рН могут быть созданы буферным раствором на основе данной протолитической пары. Поскольку 0,1 ≤ 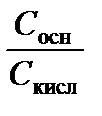 ≤ 10, величина рН данного буферного раствора должна принадлежать интервалу (р Kа ± 1). Это и есть область буферного действия протолитической пары. Для приготовления раствора с данным рН выбирают протолитическую пару, р Kа которой отличается от рН не более чем на единицу; затем, пользуясь уравнением (3.40), рассчитывают необходимое соотношение концентраций сопряженных кислоты и основания (пример 3.8).
≤ 10, величина рН данного буферного раствора должна принадлежать интервалу (р Kа ± 1). Это и есть область буферного действия протолитической пары. Для приготовления раствора с данным рН выбирают протолитическую пару, р Kа которой отличается от рН не более чем на единицу; затем, пользуясь уравнением (3.40), рассчитывают необходимое соотношение концентраций сопряженных кислоты и основания (пример 3.8).
Объясним механизм буферного действия смеси слабых сопряженных протолитов. Как следует из уравнения (3.40), разбавление такого раствора не должно влиять на его рН. Ведь при разбавлении концентрации кислоты и основания уменьшатся в одинаковое число раз, а отношение их концентраций останется постоянным[3]. При добавлении сильных протолитов с ними реагирует один из компонентов буферного раствора, в результате чего взамен сильной кислоты в растворе образуется эквивалентное количество слабой кислоты, вместо сильного основания – слабое основание. В этом случае рН меняется, но это изменение незначительно, буферный раствор смягчает действие добавленного протолита. Рассчитать рН образовавшегося раствора можно, используя уравнение (3.40), которое удобно записать не через концентрации, а через количества веществ (компонентов буфера):
рН = р Kа + lg 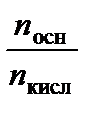 .
.
При добавлении n молей сильной кислоты величина рН изменится:
рН = р Kа + lg 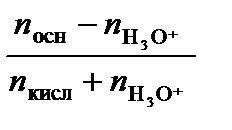 .
.
При добавлении n молей сильного основания:
рН = р Kа + lg 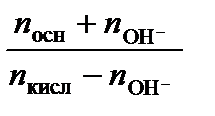 .
.
Устойчивость величины рН буферного раствора характеризует его буферная емкость p – отношение концентрации добавленного сильного протолита к изменению рН в результате добавления этого протолита:
p = 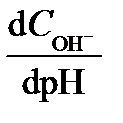 = –
= –  . (3.41)
. (3.41)
Знак (–) учитывает уменьшение рН раствора при добавлении кислоты. Физический смысл буферной емкости: она равна числу молей сильного протолита, добавление которого к 1 л буферного раствора приведет к изменению рН на единицу. Расчет буферной емкости проводят по формуле:
p = 2,3 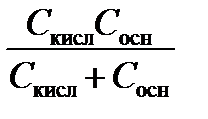 . (3.42)
. (3.42)
Анализ уравнения (3.42) показывает, что буферная емкость максимальна (а значит, рН раствора меняется слабо) при равных концентрациях сопряженных протолитов С кисл= С осн, при этом рН = р Kа. Суммарная концентрация обоих протолитов должна быть достаточно большой.Это учитывают при приготовлении буферных растворов.
Пример 3.8. Найти рН раствора, полученного при смешивании равных объемов 1 М раствора аммиака и 0,75 М раствора сульфата аммония. Как изменится рН при добавлении к 1 л такого раствора 50 мл 0,2 М раствора соляной кислоты?
Решение. Для расчета используем уравнение (3.40). Величина р Kа (NH4+) = 14,00 – р Kb (NH3) = 14,00 – 4,76 = 9,24. С учетом увеличения объема (вдвое) при смешивании растворов и соответствующего уменьшения концентраций С осн = 0,5 моль/л, С кисл= С (NH4+) = 2 С (NH4)2SO4 = 0,75 моль/л.
рН = р Kа + lg 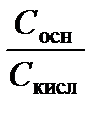 = 9,24 + lg
= 9,24 + lg  = 9,07.
= 9,07.
1 л такого раствора содержит 0,5 моль NH3 и 0,75 моль NH4+. Добавлено  = 0,2 · 0,05 = 0,01 моль НСl. Рассчитаем рН получившегося раствора по уравнению (3.41):
= 0,2 · 0,05 = 0,01 моль НСl. Рассчитаем рН получившегося раствора по уравнению (3.41):
рН = р Kа + lg 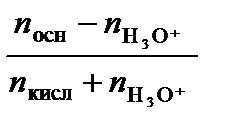 = 9,24 + lg
= 9,24 + lg  = 9,05.
= 9,05.
При добавлении соляной кислоты рН раствора уменьшится незначительно, всего на 0,02 единицы рН.
Пример 3.9. Как приготовить буферный раствор с рН 5,00 и буферной емкостью не менее 1?
Решение. Прежде всего, необходимо подобрать протолитическую пару с р Kа 4–6. Подходящей является, например, пара СН3СООH, СН3СОО–, для которой р Kа = 4,76. Соотношение концентраций компонентов раствора найдем по уравнению (3.40):
lg  = рН – р Kа = 5,00 – 4,76 = 0,24;
= рН – р Kа = 5,00 – 4,76 = 0,24;
 = 100,24 = 1,74; С осн = 1,74 С кисл.
= 100,24 = 1,74; С осн = 1,74 С кисл.
Чтобы буферная емкость составила p ³ 1, решим неравенство:
p = 2,3 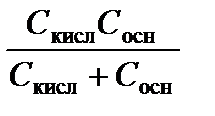 = 2,3
= 2,3 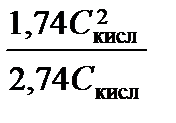 ³ 1;
³ 1;  ³ 0,684 моль/л.
³ 0,684 моль/л.
Условию удовлетворяет раствор с С (СН3СООH) = 0,684 моль/л и С (СН3СООNa) = 0,684 ∙ 1,74 = 1,19 моль/л, а также более концентрированные растворы, в которых 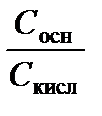 = 1,74. Приготовить такие растворы можно, рассчитав и точно измерив объем концентрированной уксусной кислоты и навеску ацетата натрия.
= 1,74. Приготовить такие растворы можно, рассчитав и точно измерив объем концентрированной уксусной кислоты и навеску ацетата натрия.
[1] Заметим, что в теории электролитической диссоциации для объяснения поведения солей потребовалась особая концепция гидролиза. А для объяснения основных свойств аммиака пришлось постулировать образование гидроксида аммония (NH4OH) и его последующую диссоциацию, хотя это соединение так и не было обнаружено в водных растворах аммиака.
[2] Часто используют символ α без дополнительного индекса, но так обозначают и мольную долю, а эти характеристики не всегда совпадают.
[3] Это верно для не слишком разбавленных растворов; сильное разбавление может несколько сместить равновесие за счет побочных процессов.






