(7.93)
Аналогичным путем можно получить и уравнение Бернулли. Оно имеет вид:
(7.94)
Расчет лопаточных решеток или межлопаточных каналов вращающихся рабочих колес удобно производить в относительном движении, так как появляется возможность использовать богатые материалы по исследованию неподвижных решеток и каналов. Но при этом возникает вопрос, насколько правомерен переход из неподвижной системы координат во вращающуюся, т.е. переход от абсолютного движения к относительному. Ответ на этот вопрос вытекает из формул (7.93) и (7.94).
Если, например, в осевой турбомашине течение происходит по цилиндрическим поверхностям, т.е. радиус линии тока на входе и выходе одинаков, то u=соnst, du=0, следовательно, формулы (7.93) и (7.94) принимают такой же вид, как обычное уравнение энергии и уравнение Бернулли для абсолютного движения. Тогда все расчеты можно вести по обычным формулам, заменяя в них абсолютную скорость с на относительную w. Если же радиус линии тока на входе и выходе неодинаков, т.е. u≠соnst, то в уравнениях необходимо учитывать изменение величины u2 /2. При Qe=0 и u=соnst уравнения энергии (7.92) и (7.93) приобретают вид, соответствующий энергоизолированному потоку, следовательно, относительное движение является энергоизолированным, несмотря на то, что абсолютное происходит с подводом или отводом механической работы. Если ввести понятие температуры торможения в относительном движении[8]
(7.95)
то, преобразовав формулу (7.92) к виду
cp (t1*– t2*) – (u 12 – u 22)/2 = 0,
нетрудно заметить, что для рассматриваемого случая (u=соnst, Qe=0) 
= соnst. Это объясняется тем, что при u=соnst на поток в межлопаточном канале не действуют никакие массовые силы, кроме сил тяжести, которыми обычно пренебрегают. Если u≠соnst, то изменяется, т.е. в относительном движении к газу подводится или отводится механическая работа, равная (u12–u22)/2. Это есть работа центробежных сил.
Значения термодинамических параметров состояния газа р, ρ, Т, а следовательно, и скорости звука а = 
, не зависят от того, в каком движении — абсолютном или относительном — они рассматриваются. Этим свойством можно воспользоваться при установлении зависимости между Т* и . Действительно
откуда
или, с учетом выражения (7.89),
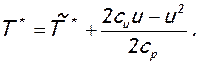(7.96)
Относительная скорость w, достигшая в каком–либо сечении величины местной скорости звука, называется критической скоростью в относительном движении. Она обозначается 
. Положив в (7.95) w= и Т=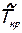 
, получим
(7.97)
Эта формула имеет такой же вид, как и для абсолютного движения. Заметим, что не изменяется также вид формул для критических отношений давлений и плотностей
(7.98)
(7.99)
Из формулы (7.97) и формулы скорости звука а = легко получается выражение для , имеющее тот же вид, что и для акр а именно:
(7.100)
Вполне понятно тогда, что не должен изменяться и вид формул связи критической скорости, максимальной скорости в относительном движении и скорости звука. Простой проверкой нетрудно убедиться, что
(7.101)
и
(7.102)
В относительном движении, так же как и в абсолютном, удобно пользоваться безразмерными скоростями — числом 
(7.103)
и приведенной скоростью 
(7.104)
Они связаны между собой такой же зависимостью, как и в абсолютном движении (см. формулы (2.54) и (2.55)).
Параметры торможения в относительном движении 
, 
и 
при помощи газодинамических функций торможения 
, 
и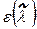 
(см. формулы (2.59), (2.60) и (2.61)) связываются с термодинамическими параметрами р, Т, ρ, только в качестве аргумента в газодинамических функциях нужно брать приведенную скорость в относительном движении 
. Это же можно сделать и при помощи формул (2.56), (2.57), (2.58), в которых число М берется в относительном движении .
Нужно заметить, что параметры торможения в относительном движении имеют вполне определенный физический смысл. Если датчики давления торможения и температуры торможения укрепить непосредственно в межлопаточном канале вращающегося колеса, то соединенные с ними приборы покажут величины и .
Формулу массового расхода
mсек = ρ w F
путем преобразований нетрудно привести к следующему виду:
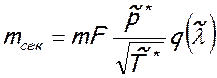(7.105)
или
(7.106)
Следовательно, и расходные функци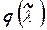и 
и 
могут быть использованы в расчетах относительного движения так же, как и абсолютного.
Из всего изложенного следует, что пользуясь критической скоростью , приведенной скоростью , параметрами торможения , , , можно рассчитывать газовый поток во вращающейся системе координат теми же методами, что и в абсолютном движении. При этом, если Qе=0 и и=соnst, то поток рассчитывается как энергоизолированный: =соnst, =соnst, для идеального газа или 
для течения с потерями.
Чтобы этим методом можно было пользоваться практически, надо дать еще формулы связи между параметрами абсолютного и относительного движения. Для температур торможения такая связь была установлена формулой (7.96). Для критических скоростей ее можно получить из соотношения
откуда
(7.107)
