Пусть функции f(x) и g(x) такие, что 
х 
(a;b).
Тогда функция f(x)-g(x)=const)
Теорема Коши. (б.д.)Пусть имеются две функции f(x) и g(x), удовлетворяющие условиям:
1) f(x) и g(x) определены и непрерывны на отрезке [a;b];
2) f(x) и g(x) имеют конечные производные 
и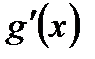 
хотя бы в интервале (a;b);
3) 
.
Тогда между точками a и b найдется по крайней мере одна точка с такая, в которой имеет место равенство: 
- формула Коши.
Доказательство. Установим сначала, что знаменатель не равен нулю, т.е. g(a)≠g(b). Действительно, если предположить, что g(a)=g(b), то функция g(x) будет удовлетворять условиям теоремы Ролля. Тогда найдется хотя бы одна точка 
такая, что 
=0. А это невозможно, т.к. по условию .
Рассмотрим вспомогательную функцию
F(x)=f(x)-f(a)- 
, которая удовлетворяет условиям теоремы Ролля, а именно 1) определена и непрерывна на отрезке [a;b], т.к. f(x) и g(x) определены и непрерывны на отрезке [a;b];
2) имеет конечную производную 
хотя бы в интервале (a;b),.т.к. в (a;b) существуют конечные производные и ;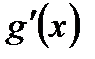
3) F(а)=f(а)-f(a)- 
=0=F(b)=f(b)-f(a)- 
=0
Следовательно, обязательно найдется хотя бы одна точка сÎ(a;b): 
, т.е.
Þ 
ч.т.д.
Замечание 1. Формула конечных приращений Лагранжа является частным случаем формулы Коши при g(x)=x, xÎ[a,b].
Замечание 2. Как формула Коши, так и формула Лагранжа, имеет место не только когда a<b, но и в случае, когда a>b
