Пусть 1) функция y=f(x) определена и непрерывна на отрезке [a;b], 2) существует конечная производная  (х), по крайней мере, на интервале (a;b), тогда найдется по крайней мере одна точка с
(х), по крайней мере, на интервале (a;b), тогда найдется по крайней мере одна точка с  (a;b) такая, что
(a;b) такая, что
 с
с  (a;b): что f(b)-f(a)=
(a;b): что f(b)-f(a)=  (c)(b-a)
(c)(b-a)
или 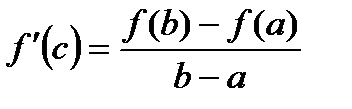
Доказательство.
1. При f(a)=f(b) утверждение вытекает из теоремы Ролля. (0=0(b-a))
2. При f(a)≠f(b). Введем вспомогательную функцию.
h 6DHaNwjkYXtpiAS+OIaPBQwqGLmCVzYZQ+SohohKzRu5oskVDHft5Ixh3z4q1PGF5YqeRh4OIQAI 0Y/uRjkpQ3zlzEDByBB57ZuRIUeVIepOqK9FhujoPCrDdZWkcMXVmngfpv43lPULQF/9CwAA//8D AFBLAwQUAAYACAAAACEAgJBuON8AAAAIAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBCF74L/ YRnBm92k2qTEbEop6qkItoJ422anSWh2NmS3SfrvnZ7saXi8x5vv5avJtmLA3jeOFMSzCARS6UxD lYLv/fvTEoQPmoxuHaGCC3pYFfd3uc6MG+kLh12oBJeQz7SCOoQuk9KXNVrtZ65DYu/oeqsDy76S ptcjl9tWzqMokVY3xB9q3eGmxvK0O1sFH6Me18/x27A9HTeX3/3i82cbo1KPD9P6FUTAKfyH4YrP 6FAw08GdyXjRsl6knLxeEGy/LNMExEHBPIlSkEUubwcUfwAAAP//AwBQSwECLQAUAAYACAAAACEA toM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQA BgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQA BgAIAAAAIQC0brs5OwkAAEhUAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQIt ABQABgAIAAAAIQCAkG443wAAAAgBAAAPAAAAAAAAAAAAAAAAAJULAABkcnMvZG93bnJldi54bWxQ SwUGAAAAAAQABADzAAAAoQwAAAAA " o:allowincell="f">
Вычтем из функции f(x) линейную функцию φ(х) такую, чтобы значение разности f(x)-φ(х) на концах отрезка совпадали.
Проведем прямую L׀׀AB, тогда
φ(х)= 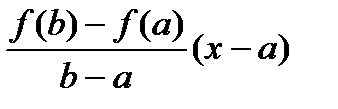
Тогда f(а)-φ(а)= f(а)-0= f(а)
f(b)-φ(b)=f(b)-f(b)+f(a)=f(a)
Введем функцию g(x)=f(x)- 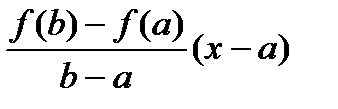 ,
,
g(a)=f(a)=g(b)
Функция g(x) удовлетворяет условиям теоремы Роля: непрерывна в [a;b], т.к. представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (a;b) имеет конечную производную, равную  (х)=
(х)=  (х)-
(х)-  . Следовательно, модно применить теорему Роля, т.е.
. Следовательно, модно применить теорему Роля, т.е.
 с
с  (a;b): что
(a;b): что  (c)=0
(c)=0
 (c)=
(c)=  (с)-
(с)-  =0, т.е.
=0, т.е. 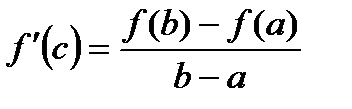 ч.т.д.
ч.т.д.
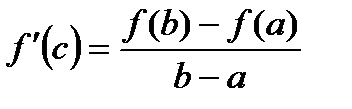 - формула Лагранжа или формула конечных приращений.
- формула Лагранжа или формула конечных приращений.
Геометрический смысл теоремы Лагранжа. Пусть A(a,f(a)) и B(b,f(b)) – концы графика функции y=f(x), АВ – хорда, соединяющая точки А и В. Тогда правая часть формулы
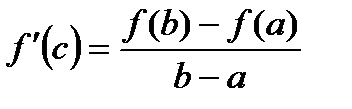
представляет собой tg b, т.е. тангенс угла, образованного хордой АВ с положительным направлением оси Ох.
Поэтому равенство 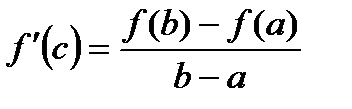 можно переписать в виде tg b=tg a. Значит, на кривой АВ имеется, по крайней мере, одна точка (c,f(c)) такая, в которой касательная к АВ параллельна хорде АВ.
можно переписать в виде tg b=tg a. Значит, на кривой АВ имеется, по крайней мере, одна точка (c,f(c)) такая, в которой касательная к АВ параллельна хорде АВ.
 (х), по крайней мере, на интервале (a;b), тогда найдется по крайней мере одна точка с
(х), по крайней мере, на интервале (a;b), тогда найдется по крайней мере одна точка с  (a;b) такая, что
(a;b) такая, что с
с  (a;b): что f(b)-f(a)=
(a;b): что f(b)-f(a)=  (c)(b-a)
(c)(b-a)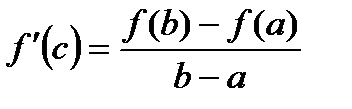
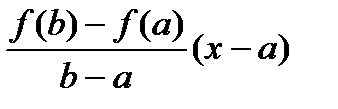
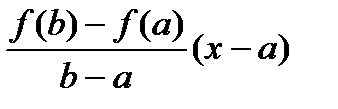 ,
, (х)=
(х)=  (х)-
(х)-  . Следовательно, модно применить теорему Роля, т.е.
. Следовательно, модно применить теорему Роля, т.е. с
с  (a;b): что
(a;b): что  (c)=0
(c)=0 (c)=
(c)=  (с)-
(с)-  =0, т.е.
=0, т.е. 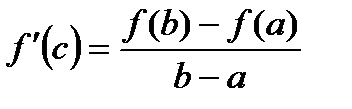 ч.т.д.
ч.т.д.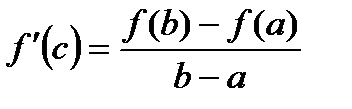 - формула Лагранжа или формула конечных приращений.
- формула Лагранжа или формула конечных приращений.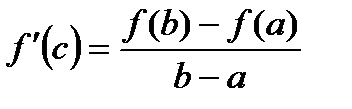 представляет собой tg b, т.е. тангенс угла, образованного хордой АВ с положительным направлением оси Ох.
представляет собой tg b, т.е. тангенс угла, образованного хордой АВ с положительным направлением оси Ох.
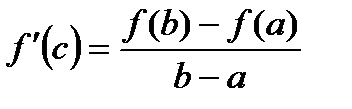 можно переписать в виде tg b=tg a. Значит, на кривой АВ имеется, по крайней мере, одна точка (c,f(c)) такая, в которой касательная к АВ параллельна хорде АВ.
можно переписать в виде tg b=tg a. Значит, на кривой АВ имеется, по крайней мере, одна точка (c,f(c)) такая, в которой касательная к АВ параллельна хорде АВ.





