Основные теоремы дифференциального исчисления.
Определение. Точка х0 называется точкой локального максимума (минимума) функции f(x), если существует такая окрестность точки х0, что для всех точек х из этой окрестности справедливо неравенство:
V(x0): 
x 
V(x0)\{x0} 
f(x)≤f(x0) (f(x)≥f(x0))
Или f(x0+∆х)≤f(x0) (f(x0+∆х)≥f(x0))
Если выполняется неравенство f(x0+∆х)<f(x0) (f(x0+∆х)>f(x0)),
То говорят, о строгом локальном максимуме (минимуме).
Значение функции в точке х0 называют максимумом (минимумом) функции.
Максимум и минимум функции называют экстремумом, х0 – точка локального экстремума.
Теорема Ферма. ( Необходимое условие экстремальных точек ) Пусть функция f(x) определена на интервале (a;b) и в некоторой точке х0 этого интервала имеет наибольшее или наименьшее значение (локальный экстремум). Тогда, если в точке х0 существует производная, то она равна нулю 
=0
Доказательство. Пусть для определенности в точке х0 функция имеет наибольшее значение, т.е. f(x)≤f(x0) 
.
Это значит, что ∆у=f(x0+∆х)-f(x0)≤0 для любой точки x0+∆х 
.
Поэтому, если ∆x>0 (x>x0),то 
.
Следовательно,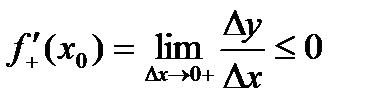 
Если же ∆x<0 (x<x0),то 
.
Поэтому, 
Т.е. правая производная в точке х0 неположительная, а левая неотрицательна. По условию существует. Значит, 
= 
= =0. Ч.т.д.
Геометрическая интерпретация теоремы Ферма состоит в том, если в точке x0 .функция f(x) принимает наибольшее или наименьшее значение, то касательная к графику функции у=f(x) в точке (х0,f(x0)) параллельна оси Ох. (Рисунок).
Теорема Ролля. Пусть функция y=f(x) определена и непрерывна на отрезке [a;b], дифференцируема хотя бы в интервале (a;b).
Если f(a)=f(b), то найдется, по крайней мере, одна такая точка с 
(a;b), что 
=0.
Доказательство.
Т.к. функция y=f(x) непрерывна на отрезке [a;b], то по теореме Вейерштрасса, функция f(x) на отрезке [a;b] достигает как своего наибольшего М, так и своего наименьшего m значения. Значит 
хÎ[a,b] Þm£f(x)£M (1)
Возможны 2 случая
1) Если m=M, то из неравенства (1) следует, что все значения функции f(x) в промежутке [a;b] равны между собой, т.е. f(x)=const, тогда с – любая точка интервала (a;b).
2) m<M, т.е. f(x)≠const. В этом случае хотя бы одно из двух значений m или M функция f(х) принимает во внутренней точке с (a;b) (иначе, ввиду того, что f(a)=f(b), мы получили бы m=M, а это не так).
Т.о. выполнены все условия теоремы Ферма. Значит =0. Ч.т.д.
