В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ, а также при умножении и делении. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ. К кодам выдвигаются следующие требования:
1) Разряды числа в коде жестко связаны с определенной разрядной сеткой.
1) Для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд.
Например, если за основу представления кода взят один байт, то для представления числа будет отведено 7 разрядов, а для записи кода знака один разряд.
Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.
Знаковым разрядом обычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт
Пример. В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа -1101 прямой код 1,0001101.
Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Пример.
Для числа +1101 прямой код 0,0001101; обратный код 0,0001101.
Для числа -1101 прямой код 1,0001101; обратный код 1,1110010.
Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы
Пример. Для числа +1101:
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
Для числа -1101:
| Прямой код | Обратный код | Дополнительный код |
| 1,0001101 | 1,1110010 | 1,1110011 |
Сложим числа, используя коды:
Прямой код
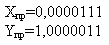
| Сложение с применением обратного кода

|
Сложение с применением дополнительного кода

Так как результат сложения является кодом положительного числа (знак 0),
то (X+Y)обр=(X+Y)доп=(X+Y)пр.
б) X= -101,Y= -11;
Сложим числа, пользуясь правилами двоичной арифметики:

Сложим числа, используя коды:
Прямой код

| Сложение в обратном коде

|
|
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код:
- из обратного кода
(X+Y)обр=1,1110100  (X+Y)пр=1,0001011;
(X+Y)пр=1,0001011;
- из дополнительного кода
(X+Y)доп=1,1110101  (X+Y)пр=1,0001010+0,0000001=1,0001011.
(X+Y)пр=1,0001010+0,0000001=1,0001011.
Таким образом, X+Y= -1011 и полученный результат совпадает с обычной записью.







