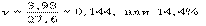Уравнение прямой при аналитическом выравнивании ряда динамики имеет следующий вид: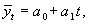 
где 
- выровненный (средний) уровень динамического ряда; a0, a1 - параметры искомой прямой; t- обозначение времени.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a 0 и a 1:
где у ¾ исходный уровень ряда динамики; n ¾ число членов ряда.
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась нулю, т. е. начало времени перенести в середину рассматриваемого периода.
Если 
то 
Исследование динамики соц.-экон. явлений и установление основной тенденции развития дают основание для прогнозирования (экстраполяции) ¾ определения будущих размеров уровня экономического явления. Используют следующие методы экстраполяции:
■ средний абсолютный прирост ¾ с/показатель, исчисляемый для выражения средней скорости роста (снижения) соц.-эк. процесса. Определяется по формуле: 
■ средний темп роста;
■ экстраполяцию на основе выравнивания по какой-либо аналитической формуле.Метод аналитического выравнивания-метод исследования динамики соц.-экон. явлений, позволяющий установить основные тенденции их развития.
Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на ПримерЕ 4.1. Исходные и расчетные данные определения параметров уравнения прямой:
Расчет необходимых значений дан в таблице примера. По итоговым данным определяем параметры уравнения:
Уравнение прямой будет иметь вид: 
Подставляя в уравнение принятые обозначения t, вычислим выровненные уровни ряда динамики (см. значения 
в табл.).
На основе данных таблицы рассчитаем показатели колеблемости динамических рядов, которые характеризуются средним квадратическим отклонением и коэффициентом вариации.
Среднее квадратическое отклонение можно измерить по формуле: 
Рассчитаем показатель колеблемости урожайности зерновых культур за анализируемый период:
Коэффициент вариации исчисляется по формуле: 
В нашем примере: 
