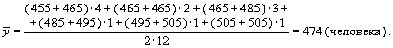Аналитические показатели уровня ряда получаются сравнением уровней между собой. Сравниваемый уровень принято называть текущим, а уровень, с которым происходит сравнение, ¾ базисным. За базу сравнения обычно принимают предыдущий уровень или начальный уровень ряда динамики.
При сравнении каждого уровня с предыдущим получаются цепные показатели. Если же сравнение ведется с одним уровнем (базой), то показатели называются базисными.
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют с/показатель ¾ абсолютный прирост (D y). Его величина определяется как разность двух сравниваемых уровней и вычисляется:
D y = уi - у 0 ¾ базисные показатели; D y = уi - уi - 1 ¾ цепные показатели,
где уi ¾ уровень i -го периода (кроме первого); у 0 ¾ уровень базисного периода; уi - 1 ¾ уровень предыдущего периода.
Пример 2.1 Имеются следующие данные о динамике производства тканей в одном из регионов за 1999–2003 гг.:
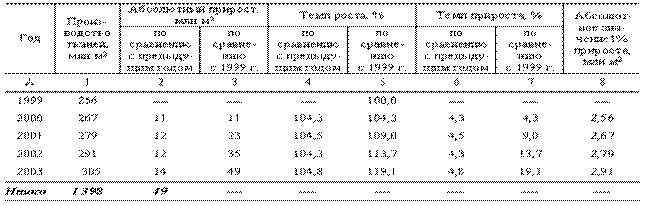
В примере 1 абсолютный прирост по сравнению с 1999 г. составит:
■ в 2000 г. ¾ D y = 267 - 256 = 11 (млн м2);
■ в 2001 г. ¾ D y = 279 - 256 = 23 (млн м2) и т. д.
Рассчитаем цепные показатели абсолютного прироста для примера 1. Абсолютный прирост составит:
■ в 2000 г. по сравнению с 1999 г. ¾ D y = 267 - 256 = 11 (млн м2);
■ в 2001 г. по сравнению с 2000 г. ¾ D y = 279 - 267 = 12 (млн м2) и т. д.
Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному. Этот показатель называется коэффициентом роста, или темпом роста (Т р), и выражается в процентах:
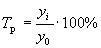¾базисные показатели; 
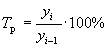¾цепные показатели.
Если Т р больше 100%, уровень растет, если меньше ¾ уровень уменьшается. Т р ¾ всегда положительное число.
В примере 1 темп роста составит:
■в 2000г. по сравнению с базисным 1999 г.: 
■в 2001г. по сравнению с базисным 1999 г.: 
Рассчитаем цепные показатели темпа роста для примера 1. Темп роста составит:
■в 2000 г. по сравнению с базисным 1999 г.: 
■в 2001 г. по сравнению с 2000 г.: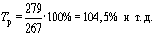 
Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Т пр), который рассчитывается как отношение абсолютного прироста к базисному или предыдущему уровню:
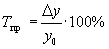¾базисные показатели; 
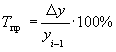¾цепные показатели.
Темп прироста может быть вычислен также путем вычитания из темпов роста 100%, т. е. Т пр = Т р - 100%.
Для примера 1 рассчитаем темп прироста:
■ в 2000 г. по сравнению с базисным 1999 г.: T пр = 104,3% - 100% = 4,3%;
■ в 2001 г. по сравнению с базисным 1999 г.: T пр = 109% - 100% = 9% и т. д.
Показатель абсолютного значения 1% прироста (|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в %.
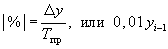или 0,01 yi - 1.
В примере 1 абсолютное значение прироста 1% составит:
■ в 2000 г. по сравнению с 1999 г.: |%| = 0,01 y 1999 г. = 0,01 × 256 = 2,56 (млн м2);
■ в 2001 г. по сравнению с 2000 г.: |%| = 0,01 y 2000 г. = 0,01 × 267 = 2,67 (млн м2) и т. д.
Приведенная в примере 1 таблица с вычислениями характеристик изменения уровней позволяет проводить анализ данного динамического ряда.
В примере 1 мы имеем интервальный ряд динамики с равноотстоящими уровнями во времени, поэтому средний уровень ряда рассчитаем по формуле средней арифметической простой:
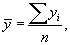где 
¾итог суммирования уровней за весь период; n ¾ число периодов.
Средний объем производства тканей за пять лет составил: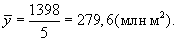 
Средний абсолютный прирост определяется по формуле: 
В примере 1 среднегодовой прирост производства тканей за 1999-2003 гг. равен:
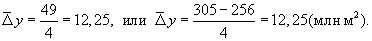
Среднегодовой темп роста вычисляется по формуле средней геометрической:
где n ¾ число коэффициентов роста.
Среднегодовой темп роста производства тканей за 1999-2003 г. (пример 1) рассчитаем двумя способами:
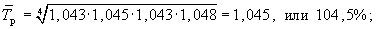
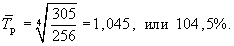
Среднегодовой темп прироста получим, вычтя из среднего темпа роста 100%. В примере 1:
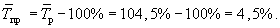
Если интервальный ряд динамики имеет неравноотстоящие уровни, то средний уровень ряда вычисляется по формуле средней арифметической взвешенной:
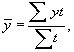где t ¾ число периодов времени, в течение которых уровень не изменяется.
Для моментного ряда с равноотстоящими уровнями средний уровень ряда вычисляется по формуле средней хронологической.
Пример 2.2 Известны товарные остатки магазина на 1-е число каждого месяца 2003 г.
В данном случае мы имеем моментный ряд с равноотстоящими уровнями, поэтому средний уровень ряда определим по формуле средней хронологической, которая рассчитывается следующим образом:
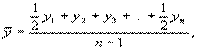где n — число уровней ряда.
Средние товарные остатки за полугодие составят: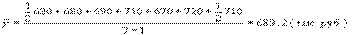 
Пример 2.3 Известна численность работников предприятия на следующие даты:
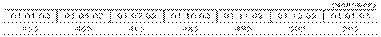
В данном случае мы имеем моментный ряд динамики с разноотстоящими уровнями, поэтому средний уровень ряда рассчитаем по формуле средней хронологической для разноотстоящих уровней динамики:
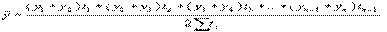
Среднесписочная численность работников составит: 
