Метод скользящей средней ¾ метод изучения в рядах динамики основной тенденции развития явления.
Суть метода скользящей средней состоит в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем ¾ средний уровень из того же числа уровней, начиная со второго, далее ¾ начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Средняя из нечетного числа уровней относится к середине интервала. Если интервал сглаживания четный, то отнесение средней к определенному времени невозможно, она относится к середине между датами. Для того чтобы правильно отнести среднюю из четного числа уровней, применяется центрирование, т. е. нахождение средней из средней, которую относят уже к определенной дате.
Покажем применение скользящей средней на следующем примере. Пример 3.1. На основе данных об урожайности зерновых культур в хозяйстве за 1989–2003 гг. проведем сглаживание ряда методом скользящей средней.
Динамика урожайности зерновых культур в хозяйстве за 1989–2003 гг. и расчет скользящих средних
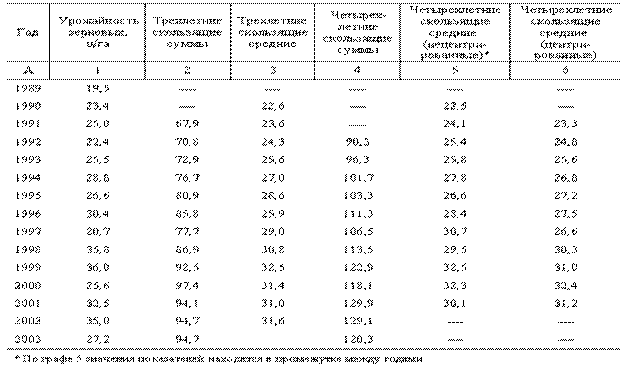
1. Рассчитаем трехлетние скользящие суммы. Находим сумму урожайности за 1989–1991 гг.: 19,5 + 23,4 + 25,0 = 67,9 и записываем это значение в 1991 г. Затем из этой суммы вычитаем значение показателя за 1989 г. и прибавляем показатель за 1992 г.: 67,9 – 19,5 + 22,4 = 70,8 и это значение записываем в 1992 г. и т. д.
2. Определим трехлетние скользящие средних по формуле простой средней арифметической:
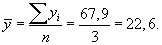
Полученное значение записываем в 1990 г. Затем берем следующую трехлетнюю скользящую сумму и находим трехлетнюю скользящую среднюю: 70,8: 3 = 23,6, полученное значение записываем в 1991 г. и т. д.
Аналогичным образом рассчитываются четырехлетние скользящие суммы. Их значения представлены в графе 4 таблицы данного примера.
Четырехлетние скользящие средние определяются по формуле простой средней арифметической:
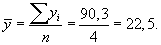
Это значение будет отнесено между двумя годами — 1990 и 1991 гг., т. е. в середине интервала сглаживания. Для того чтобы найти четырехлетние скользящие средние центрированные, необходимо найти среднюю из двух смежных скользящих средних:
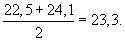
Эта средняя будет отнесена к 1991 г. Аналогичным образом рассчитываются остальные центрированные средние; их значения записываются в графу 6 таблицы данного примера.






