
Расчет на контактную прочность включает расчеты на сопротивление усталости и на предотвращение разрушения рабочих поверхностей зубьев при максимальной однократной нагрузке.
Расчет на сопротивление усталости. Разрушение от переменных контактных напряжений начинается вблизи полюса. Поэтому расчетные напряжения определяют на линии контакта, проходящей через полюс П.
Цель расчета — определение размеров передачи при выбранном материале и заданной твердости поверхности зубьев колес, при которых не будет прогрессивного выкрашивания. Условие контактной прочности записывают в виде
 .
.
где σн — расчетное напряжение, зависящее от геометрических параметров передачи и нагрузки; [σ]н — допускаемое напряжение, зависящее от материала, термообработки колес и характера нагрузки.
Контакт двух зубьев можно рассматривать как контакт двух цилиндров с радиусами кривизны ρ1 = N1П и ρ2 = N2П в полюсе зацепления П. В качестве исходной принимают формулу Герца для наибольших контактных напряжений σн на площадке контакта двух стальных цилиндров при их сжатии

Где  — распределенная нагрузка; F — нормальная к контактирующим поверхностям сила сжатия; ls, — суммарная длина контактных линий; Е — модуль упругости; ρ — приведенный радиус кривизны.
— распределенная нагрузка; F — нормальная к контактирующим поверхностям сила сжатия; ls, — суммарная длина контактных линий; Е — модуль упругости; ρ — приведенный радиус кривизны.
Для получения расчетной зависимости в удобной форме заменим величины, входящие в формулу Герца через параметры зацепления. Для прямозубой передачи нормальная результирующая сила определяется через окружную силу Ft

Суммарная длина контактных линий К1К2 в прямозубой передаче переменна. В зоне однопарного зацепления она равна b, в зоне двухпарного зацепления — 2b. Для расчетов принимают
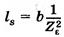 ,
,  - коэффициент, учитывающий суммарную длину контактных линий.
- коэффициент, учитывающий суммарную длину контактных линий.
Для стальных колес модуль упругости Е = 2,1 • 105 МПа, тогда коэффициент, учитывающий механические свойства материала колес, ZЕ = 191,6 МПа0,5.


Учитывая  , получаем в итоге
, получаем в итоге

Подставим все в формулу Герца

Дополнительно обозначим

ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев.

Выразим  и заменим
и заменим 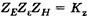

Для передач без смещения 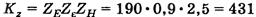 .
.
 - коэффициент относительной ширины колеса.
- коэффициент относительной ширины колеса.

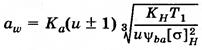
 =450 для прямозубых,
=450 для прямозубых,  =410 для косозубых.
=410 для косозубых.






