фокусами, есть величина постоянная. Величина, определяемая
как отношение фокусного расстояния к длине действительной
оси (длина отрезка, соединяющего вершины гиперболы), называется
эксцентриситетом гиперболы 
.
Из аналитической геометрии известно, что все эллипсы (кроме
окружности), параболы и гиперболы обладают следующим свойством: для
каждой из этих линий остается неизменным отношение
,
где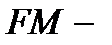 
расстояние от
произвольной её точки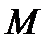 
до
данной точки 
(фокуса), а
расстояние от точки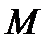
до данной прямой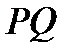 
(директрисы).
Обобщая сказанное, можно дать
общее определение конического
сечения (эллипса, гиперболы и
параболы): коническое сечение есть
геометрическое место точек, отношение
расстояний которых до данной точки
(фокуса) и до данной прямой (директрисы) есть величина постоянная 
.
При этом
для эллипса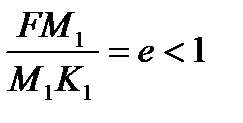 
;
для параболы 
;
для гиперболы 
.
Из (13.5) следует, что при 
эксцентриситет 
, т.е. орбита является эллипсом и движение частицы финитно. Большая и малая полуоси эллипса, согласно формулам аналитической геометрии, равны
, (13.7)
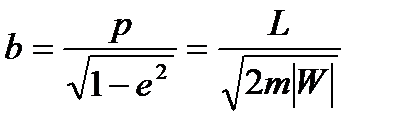. (13.8)
расстояние между фокусами эллипса.
Из уравнения (13.6) следует, что точка с 
является ближайщей к центру поля (перигелий орбиты), что, вообще говоря, является следствием сделанного выбора начала отсчета угла 
.
Наименьшее (перигелий) и наибольшее (апогей, афелий) при 
в (13.6) расстояния частицы от центра поля (фокуса эллипса) составляют
|
|
|
|
|
|
|
|
; 
(13.9)
и зависят только от энергии частицы, поскольку из (13.7),
следует, что большая полуось эллипса 
зависит только от
энергии, но не от момента импульса частицы).
Примечание. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце –
первый закон Кеплера.
Время обращения по эллиптической орбите (период 
) можно определить с помощью закона сохранения импульса частицы в форме “интеграла площадей”. Интегрируя выражение (12.8) по времени от нуля до , получаем
, (13.10)
где 
площадь орбиты. Для эллипса 
, и используя (13.7) и (13.8), находим
. (13.11)
Тот факт, что квадрат периода обращения должен быть пропорционален кубу линейных размеров орбиты, составляет содержание третьего закона Кеплера.
Отметим, что период обращения, как следует из (13.11) зависит только от энергии частицы.
При 
, когда энергия частицы достигает минимума (13.3), эллипс вырождается в окружность.
В случаях, когда энергия частицы 
, её движение инфинитно.
Если энергия частицы положительна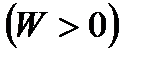 
, то эксцентриситет её орбиты 
(см. 13.5), т.е. траектория движения является гиперболой, огибающей фокус (центр поля). Расстояние перигелия от центра
поля определяется выражением
, (13.12)
|
|
|
|
|
|
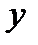
(13.13)
“полуось” гиперболы.
В случае, когда полная энергия частицы 
эксцентриситет кривой 
, т.е. частица движется по параболе,
с перигелием
. (13.14)
Этот случай реализуется, если частица начинает свое движение
из состояния покоя на бесконечности.
Используя выражения (11.17, 13.9, 13.12 и 13.14) и соответствующие значения эксцентриситета, можно найти скорость частицы в перигелии при движении по всем рассмотренным траекториям. В точке поворота (перигелии)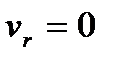 
, поэтому 
.
По окружности () будет двигаться частица, имеющая скорость
,
движению по параболе () будет соответствовать скорость
.
Если скорость частицы лежит в интервале
,
то её траекторией является эллипс ().
При
,
то траектория частицы имеет форму гиперболы (
).
В небесной механике 
и 
первая и вторая космические скорости.
Обратимся теперь к движению в поле отталкивания, в котором потенциальная энергия частицы определяется выражением
, (13.15)
где 
.
В этом случае эффективная потенциальная энергия частицы
|
|
|
|
|
|
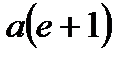
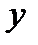
(13.16)
монотонно убывает от бесконечности до нуля 
при изменении расстояния от центра поля от нуля до
бесконечности 
. Очевидно, что полная
энергия частицы 
может быть только положительной
и её движение инфинитно. Все вычисления в этом случае
полностью аналогичны приведенным выше.
Траектория частицы является гиперболой
, (13.17)
где характеристики кривой по-прежнему определяются
выражениями (13.5).
Двигаясь по такой траектории, частица проходит мимо центра поля, как показано на рисунке. Расстояние
перигелия
. (13.18)
В заключение рассмотрения задачи Кеплера укажем, что при движении в поле центральных сил, котором потенциальная энергия частицы определяется выражением с любым знаком 
, существует интеграл движения (сохраняющийся во времени вектор), специфический именно для этого поля:
, (13.19)
что легко проверить непосредственным вычислением, взяв от него производную по времени.
Сохраняющийся вектор (13.19) направлен вдоль большой оси от фокуса к перигелию и равен по величине 
. Проще всего в этом убедиться, рассмотрев его значение в перигелии.
Интеграл движения (13.19), наряду с такими сохраняющимися величинами, как полная энергия 
и момент импульса 
частицы, является однозначной функцией состояния (положения и скорости) частицы.
