12.1. Сохранение момента импульса в центральном поле.
Выше мы ввели в рассмотрение центральные силы. Напомним, что сила называется центральной, если для всех точек поля она направлена к одной и той же точке (или от одной и той же точки) и зависит только от расстояния до этой точки, называемой центром сил, или силовым центром.
. (12.1)
Уже из определения следует, что центральные силы консервативны.
В поле консервативных сил можно ввести потенциальную энергию:
(12.2)
При движении в центральном поле момент силы равен нулю, т.к. угол между векторами в векторном произведении равен нулю:
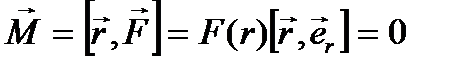. (12.3)
Тогда из уравнения моментов (11.5) получаем, что момент импульса есть постоянная величина.
При движении частицы в центральном поле полный момент импульса сохраняется, несмотря на то, что система (одна частица) не является замкнутой.
|
|
|
|
|
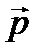
. (12.4)
Поскольку 
, т.е. величина и направление вектора
сохраняются, а вектор момента импульса всегда
перпендикулярен к векторам 
и 
, то движение частицы
происходит в плоскости, перпендикулярной к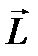 
. Отсюда следует,
что частица в поле центральных сил движется по плоской орбите.
Если ось 
направлена по вектору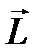 
, то 
, а траектория частицы лежит в плоскости, перпендикулярной оси . Выше мы получили, что 
, где 
проекция радиус-вектора 
на плоскость, в которой лежит траектория частицы. В рассматриваемом случае, начало координат и вектор лежит в плоскости орбиты, поэтому
. (12.5)
|
Геометрическая интерпретация.
Пусть частица движется в поле центральных сил по плоской траектории, представляющей собой замкнутую кривую.
Выбрав за начало отсчета точку 
, найдем площадь сектора 
, показанного на рисунке.
.
Здесь 
- угол между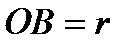 
(длина радиус-вектора, проведенного к точке 
) и 
. Будем сжимать отрезок к точке 
. В пределе 
– касательная к траектории частицы в точке , т.е. 
.
Тогда можем записать
. (12.6)
Вводя понятие секториальной скорости как площади, описываемой радиусом-вектором в единицу времени, получаем
. (12.7)
Обратим внимание, что вектор секториальной скорости и вектор 
напрвлены вдоль вектора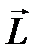 
и перпендикулярны плоскости орбиты.
Если применить выражение (12.7) к описанию движения планет, то мы получим математическое выражение 2-го закона Кеплера, устанавливающего постоянство секториальной скорости планеты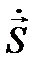 
при движении в центральном поле:
. (12.8)
Этому закону подчиняется, например, движение планет по эллиптическим орбитам.
Итак, свойства движения частицы в центральном поле:
1) движение плоское, плоскость проходит через точку 
, определенный относительно которой момент импульса частицы сохраняется.
2) секториальная скорость постоянна (II закон Кеплера).
Примечания:
Площадь 
элементарного сектора, описываемая радиус-вектором при повороте на 
за время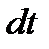 
:
.
Закон сохранения момента импульса частицы, движущейся в центральном поле иногда называют “интегралом площадей”.
12.2. Закон сохранения энергии в центральном поле.
Центральные силы консервативны, следовательно, полная энергия частицы в системе «силовой центр – частица» (замкнутая система) сохраняется.
. (12.9)
Поскольку задача плоская, удобно воспользоваться полярными координатами и представить импульс частицы в виде суммы радиальной и азимутальной составляющих:
|
|
|
|
|
.
В полярных координатах выражения для момента импульса и полной энергии 
частицы приобретают вид:
; (12.10)
. (12.11)
В выражении (12.10) 
, т.к. 
, и
, (12.10а)
т.к. траектория частицы плоская и 
.
Если, воспользовавшись (12.10), исключить из уравнения (12.11) азимутальную составляющую импульса частицы 
, то полную механическую энергию частицы можно записать как
. (12.12)
Примечание. Величину 
называют центробежной энергией.
Уравнение (12.12) содержит только одну неизвестную – радиальную компоненту импульса 
. Поэтому оно может формально рассматриваться как уравнение для энергии одномерного – радиального – движения частицы. В этом случае роль потенциальной энергии играет функция
. (12.13)
Т.о., можно сказать, что задача о движении частицы в центральном поле сводится к нахождению условий финитности (инфинитности) одномерного движения частицы в радиальном направлении в поле, описываемом эффективной потенциальной функцией 
.
12.3. О траектории движения частицы.
Найдем уравнение траектории частицы, движущейся в поле центральных сил.
Представим компоненты импульса, записанного в полярных координатах, следующим образом:
(12.14)
Далее, т.к. угол между вектором угловой скорости 
и радиус-вектором 
равен 
, то
.
Тогда из (12.10а, 12.12 и 12.14) для энергии и момента импульса частицы, движущейся в центральном поле, получаем
. (12.15)
Из первого уравнения (12.15) получаем
.
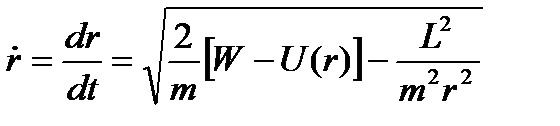Разделяя переменные, находим в неявном виде зависимость 
:
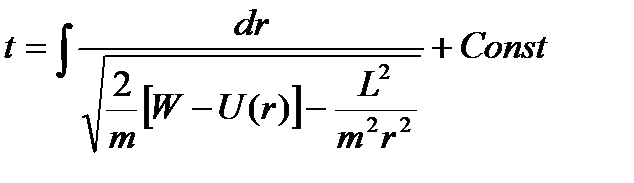. (12.16)
Из второго уравнения (12.15) имеем
.
Исключив из уравнений (12.15) время 
, находим уравнение траектории частицы в центральном поле в полярных координатах (связь между 
и 
):
. (12.17)
Интегралы (12.16) и (12.17), вообще говоря, могут быть вычислены, если известен явный вид функции 
.
12.4. Границы движения.
Из первого уравнения (12.15) следует, что значения , при которых энергия частицы равна
, (12.18)
определяют границы области движения по расстоянию от центра поля, поскольку при выполнении равенства (12.18) радиальная скорость 
обращается в нуль. Однако равенство нулю (
) радиальной составляющей скорости не означает, что частица остановилась, т.к. азимутальная (угловая) компонента скорости отлична от нуля (
). Это утверждение вытекает из требования 
для поля центральных сил.
Равенство 
определяет “точку поворота” траектории, в которой функция 
достигает либо максимального, либо минимального значения, после чего начинает соответственно убывать или возрастать.
Если область допустимого изменения ограничена лишь условием 
, то движение частицы инфинитно – её траектория приходит из бесконечности и уходит на бесконечность.
Если область изменения имеет две границы 
и 
, то движение является финитным и траектория частицы лежит внутри кольца, ограниченного окружностями 
и 
, определяющими границы движения. Однако траектория при этом может оставаться незамкнутой.
За время прохождения одной петли (от до и снова до ) радиус-вектор частицы совершит поворот на угол
. (12.19)
Условие замкнутости траектории: траектория будет замкнутой, если 
, где 
и 
- целые
числа, т.е. за одну петлю радиус-вектор должен повернуться
на угол, равный рациональной части от 
.
Тогда через 
повторений этого периода времени радиус-
вектор точки, сделав 
полных оборотов, совпадет со своим
первоначальным значением, т.е. траектория замкнется.
Однако такой исход является скорее исключением,
нежели правилом. Существуют лишь два типа центральных
полей, в которых все траектории финитных движений
замкнуты. Это поля, где зависимость потенциальной энергии
от расстояния от центра поля имеет вид:
.
13. Задача Кеплера.
Задача Кеплера (Кеплерова задача) - задача о движении частицы в поле центральных сил, убывающих обратно пропорционально квадрату расстояния от центра поля. Этому закону подчиняются силы гравитационного притяжения между точечными массами (или телами, обладающими сферической симметрией), а также кулоновские силы, действующие между точечными электрическими зарядами. Поэтому такие поля являются важнейшим случаем центральных полей.
В таком поле потенциальная энергия частицы определяется выражением
, (13.1)
где 
постоянная величина, 
расстояние от центра поля.
Рассмотрим случай, когда 
, т.е. сила, действующая на частицу, направлена к центру поля и
|
потенциальной энергии
(13.2)
|
|
стремится к 
, а при 
она стремится к нулю со стороны отрицательных
значений; при 
функция имеет минимум,
равный
. (13.3)
Из рисунка видно, что движение частицы будет инфинитным при 
, и финитным при 
.
Форму траектории получаем интегрированием формулы (12.17) после подстановки :
. (13.4)
Выбирая начало отсчета угла так, чтобы постоянная интегрирования обращалась в нуль (
), и введя обозначения
, 
, (13.5)
получим уравнение траектории в виде:
. (13.6)
Приложение. Выражение (13.6) – уравнение в полярных координатах конического сечения с фокусом в начале
координат 
; 
и 
так называемые параметр и эксцентриситет
орбиты, соответственно.
Коническими сечениями называют эллипс, параболу и гиперболу, т.к. их
можно получить на поверхности круглого конуса в пересечении с
плоскостью 
, не проходящей через вершину конуса. При этом
поверхность конуса предполагается неограниченно продолженной в обе
стороны от вершины.
Если плоскость 
не параллельна ни одной образующей конуса, то
коническое сечение есть эллипс. Эллипсом называется геометрическое
место точек, сумма расстояний от которых до двух данных точек,
называемых его фокусами, есть величина постоянная. Отношение фокусного расстояния эллипса к длине его большой оси называется эксцентриситетом эллипса 
.
Если плоскость параллельна только одной из образующих конуса
(
), то коническое сечение есть парабола. Параболой называют
геометрическое место точек, равноотстоящих от данной точки,
