Совокупность опытных данных указывает на то, что наряду с энергией и импульсом, существует ещё одна физическая величина, для которой в замкнутой системе тел выполняется закон сохранения, - момент импульса.
Определение: Моментом импульса частицы относительно неподвижного начала (точки 0) называют вектор  , определяемый как векторное произведение радиус-вектора
, определяемый как векторное произведение радиус-вектора  частицы на её импульс
частицы на её импульс  :
:

|
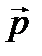
|
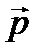
|

|

|

|
 , (11.1)
, (11.1)
где  аксиальный вектор, перпендикулярный плоскости, образуемой вектором импульса (скорости) и радиус-вектором.
аксиальный вектор, перпендикулярный плоскости, образуемой вектором импульса (скорости) и радиус-вектором.
Векторы  ,
,  и
и  образуют правовинтовую систему, поэтому чтобы определить направление вектора
образуют правовинтовую систему, поэтому чтобы определить направление вектора  , поступаем следующим образом. Совмещаем начала векторов, стоящих в скобках, и вращаем “буравчик” от первого вектора ко второму. Тогда поступательное движение “буравчика” дает направление вектора
, поступаем следующим образом. Совмещаем начала векторов, стоящих в скобках, и вращаем “буравчик” от первого вектора ко второму. Тогда поступательное движение “буравчика” дает направление вектора  .
.
Длина (модуль) вектора момента импульса равна

где  плечо вектора импульса
плечо вектора импульса  относительно точки 0. Момент импульса системы материальных точек относительно точки 0 есть векторная сумма моментов импульсов каждой из частиц относительно того же начала:
относительно точки 0. Момент импульса системы материальных точек относительно точки 0 есть векторная сумма моментов импульсов каждой из частиц относительно того же начала:
 . (11.2)
. (11.2)
11.2. Уравнение моментов.
Рассмотрим движение отдельной частицы под действием силы  в течение промежутка времени
в течение промежутка времени 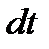 и определим, что происходит с моментом импульса этой частицы:
и определим, что происходит с моментом импульса этой частицы:

|

Первое слагаемое обращается в нуль в силу свойств векторного произведения, т.к. вектор скорости параллелен вектору импульса. Таким образом
 . (11.3)
. (11.3)
Вектор, стоящий в правой части уравнения, называется моментом силы относительно точки 0:
 . (11.4)
. (11.4)
Получаем, что механическая величина, называемая моментом силы, ответственна за изменение вектора  в данной системе отсчета.
в данной системе отсчета.
 уравнение моментов. (11.5)
уравнение моментов. (11.5)
Определение: Производная по времени от момента импульса материальной точки относительно неподвижного начала равна моменту действующей силы относительно того же начала.
Отметим, что в инерциальных системах отсчета момент силы определяется только силами взаимодействия, в неинерциальных системах наряду с силами взаимодействия необходимо учитывать также силы инерции.
Модуль вектора момента силы равен
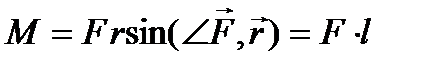 ,
,

|

|

|

|
 плечо вектора силы
плечо вектора силы  относительно точки
относительно точки  .
.
Геометрическая интерпретация векторного произведения дана на рисунке. Векторы  ,
,  и
и  образуют правовинтовую систему. Длина вектора
образуют правовинтовую систему. Длина вектора  численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах  и
и  :
:

Аналогично определяются направление и длина вектора момента силы  .
.
Уравнение моментов (11.9), как и основное уравнение динамики, позволяет решать задачи 2-х типов. 1).Определение момента сил  относительно интересующего нас начала
относительно интересующего нас начала  , если известна зависимость от времени момента импульса
, если известна зависимость от времени момента импульса  относительно той же точки
относительно той же точки  . Эта задача сводится к нахождению производной по времени от момента импульса.
. Эта задача сводится к нахождению производной по времени от момента импульса.
 .
.
2).Нахождение приращения момента импульса частицы относительно точки  , если известна зависимость от времени момента сил
, если известна зависимость от времени момента сил  , действующего на частицу, относительно того же начала. Решается интегрированием:
, действующего на частицу, относительно того же начала. Решается интегрированием:
 . (11.6)
. (11.6)
Примечание. Величину, стоящую в правой части уравнения (11.6) называют импульсом момента силы.
11.3. Закон сохранения момента импульса.
Рассмотрим произвольную систему материальных точек. Момент импульса этой системы:
 , (11.7)
, (11.7)
причем все векторы в (11.7) определены относительно одной и той же точки  .
.
Нас будет интересовать, что является причиной изменения момента импульса системы частиц. Для этого
продифференцируем (11.7) по времени
 . (11.8)
. (11.8)
Рассматривая все силы, действующие на частицы системы, как внутренние и внешние можем записать
 . (11.9)
. (11.9)

|

|
 ,
,

|

|

|
 , т.к. внутренние силы –
, т.к. внутренние силы –парные силы. Действительно, в каждой паре эти силы равны по

|

|

|
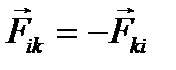
и лежат на одной прямой, т.е. имеют одинаковое плечо  (см. рисунок).
(см. рисунок).
Отсюда следует, что
 . (11.10)
. (11.10)
Итак, для системы взаимодействующих частиц уравнение
моментов имеет вид:
 . (11.11)
. (11.11)
Производная момента импульса системы материальных точек по времени равна суммарному моменту всех внешних сил, действующих на частицы системы.
Для замкнутой системы 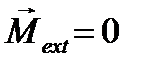 , тогда из (11.11) получаем
, тогда из (11.11) получаем
 , (11.12)
, (11.12)
т.е.
 . (11.12a)
. (11.12a)
(11.12a) выражает закон сохранения момента импульса замкнутой системычастиц.
В инерциальной системе отсчета момент импульса замкнутой системы частиц сохраняется.
Моменты импульсов отдельных частиц или частей замкнутой системы могут изменяться со временем. Однако эти изменения всегда происходят так, что приращение момента импульса одной части системы равно убыли момента импульса другой её части, относительно одной и той же точки инерциальной системы отсчета.
Наряду с законами сохранения импульса и энергии, закон сохранения момента импульса является фундаментальным законом природы.
Для одной материальной точки, если момент силы равен нулю, также получаем

11.4. Момент импульса и силы относительно оси.
Уравнение моментов (11.5) - векторное уравнение, поэтому в декартовых координатах его можно записать можно записать в виде трех скалярных уравнений:
 . (11.13)
. (11.13)
Пусть в интересующей нас системе отсчета ось  неподвижна, и точка
неподвижна, и точка  , относительно которой рассматриваются моменты, находится на этой оси.
, относительно которой рассматриваются моменты, находится на этой оси.

|
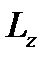
|

|

|

|

|
Моментом импульса относительно оси  называют проекцию на эту ось вектора
называют проекцию на эту ось вектора  , определенного относительно произвольной точки
, определенного относительно произвольной точки  на данной оси (см. рисунок). Аналогично определяется и момент силы относительно любой выбранной оси.
на данной оси (см. рисунок). Аналогично определяется и момент силы относительно любой выбранной оси.
Обозначим их  и
и  , тогда, спроектировав (11.5) на ось
, тогда, спроектировав (11.5) на ось  , получаем
, получаем
 , (11.14)
, (11.14)
т.е. производная по времени от момента импульса частицы относительно оси  равна моменту силы относительно той же оси.
равна моменту силы относительно той же оси.
Если
 , то
, то  ,
,
т.е. если момент силы относительно некоторой неподвижной оси  равен нулю, то момент импульса частицы относительно этой оси остается постоянным, хотя сам вектор момента импульса
равен нулю, то момент импульса частицы относительно этой оси остается постоянным, хотя сам вектор момента импульса  может меняться.
может меняться.
Найдем аналитические выражения для  и
и  , т.е. будем искать проекции на ось
, т.е. будем искать проекции на ось  векторных произведений
векторных произведений  и
и  . Эту задачу удобнее решать в цилиндрической системе координат. Поэтому
. Эту задачу удобнее решать в цилиндрической системе координат. Поэтому

|

|

|

|

|

|

|

|

|
 и
и  через координаты
через координаты 

 цилиндрической
цилиндрической
системы, связав с частицей орты 

 , направленные в сторону
, направленные в сторону
возрастания соответствующих координат:
 , (11.15)
, (11.15)
 , (11.16)
, (11.16)
где  плечо (перпендикуляр, опущенный из точки
плечо (перпендикуляр, опущенный из точки  на ось
на ось  , см.
, см.
рисунок).
Векторное произведение  можно представить с помощью
можно представить с помощью
определителя

Взяв проекцию вектора  на соответствующую ось, получаем момент импульса частицы относительно оси
на соответствующую ось, получаем момент импульса частицы относительно оси  :
:
 (11.17).
(11.17).
Если учесть, что
 ,
,
т.к. скорость  выражается через угловую скорость как
выражается через угловую скорость как  и, соответственно,
и, соответственно,  , можно привести выражение для момента импульса частицы относительно оси
, можно привести выражение для момента импульса частицы относительно оси  к виду, более удобному для практических применений:
к виду, более удобному для практических применений:
 . (11.18).
. (11.18).
Заметим, что  проекция на ось
проекция на ось  вектора угловой скорости
вектора угловой скорости  , с которой поворачивается радиус-вектор частицы.
, с которой поворачивается радиус-вектор частицы.
Аналогично записывается выражение для момента силы относительно оси  :
:
 . (11.13)
. (11.13)
Анализируя полученные выражения, можно сделать очевидный, но важный вывод: проекции  и
и  не зависят от выбора точки
не зависят от выбора точки  на оси
на оси  , относительно которой определены векторы
, относительно которой определены векторы  и
и  . Кроме того,
. Кроме того,  и
и  - алгебраические величины, знаки которых соответствуют знакам проекций
- алгебраические величины, знаки которых соответствуют знакам проекций  и
и  .
.






