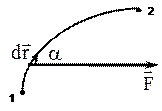Пусть материальная точка под действием силы 
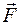совершает перемещение по некоторой траектории из точки 1 в точку 2. При этом в общем случае сила 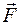может изменяться в процессе движения, как по величине, так и по направлению. Рассмотрим элементарное перемещение 
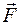, в пределах которого силу можно считать постоянной.
Механической работой называется скалярная величина, равная скалярному произведению 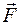на : 
, где α – угол между векторам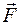и и .
В СИ единицей измерения работы является джоуль (1 Дж = 1 Н.м).
Для нахождения полной работы на участке 1-2 необходимо проинтегрировать выражение: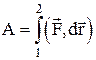 
.
Соотношение справедливо не только для материальной точки, но и для любого тела или системы тел. Если построить график зависимости силы от пройденного пути, то элементарная работа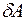 
численно равна площади заштрихованной полоски: 
, где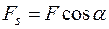 
.
Полная работа на пути от точки 1 до точки 2 равна площади всей криволинейной трапеции.
Для получения формулы для работы внешних сил при вращательном движении рассмотрим вначале случай действия на материальную точку массой m касательной силы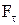 
, которая вызывает ее перемещение по дуге 
. Элементарная работа: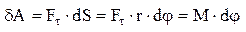 
.
Средняя мощность – работа, совершаемая за единицу времени: 
. Мгновенная мощность: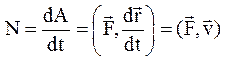 
, где 
– скорость точки приложения силы.
В СИ единицей измерения мощности является ватт (1 Вт = 1 Дж/с).
Состояние тела или системы тел характеризуется величиной, называемой энергия.
Энергия – универсальная мера различных форм движения и взаимодействий материи. Существуют различные виды энергии: механическая, тепловая, электромагнитная и т.д.
Механическая энергия – это величина, характеризующая максимальную работу, которую тело может совершить.
В системе СИ энергия измеряется в джоулях (Дж), как и работа.
Кинетическая энергия – это энергия, обусловленная движением тела. Пусть частица массы m движется под действием некоторой силы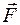 
вдоль оси x. Элементарная работа, совершаемая этой силой: 
, однако 
и 
. Следовательно, полная работа, совершаемая силой 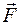при перемещении частицы из точки 1 в точку 2: 
.
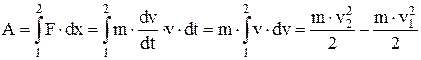Величина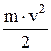 
называется кинетической энергией. 
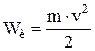. Работа силы, действующей на материальную точку, равна изменению кинетической энергии этой материальной точки 
.
Если совершаемая работа положительна (A>0), кинетическая энергия растет, в противном случае она убывает.
Это утверждение справедливо и для системы тел (материальных точек), если под работой понимать работу внешних сил, а кинетическую энергию системы материальных точек определить как сумму кинетических энергий всех точек, входящих в систему: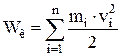 
.
Кинетическая энергия тела вращающегося вокруг закрепленной оси представляет собой алгебраическую сумму кинетических энергий отдельных его точек: 
. Таким образом, кинетическая энергия вращающегося тела: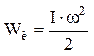 
.
Работа внешних сил при вращательном движении также затрачивается на изменение кинетической энергии: 
, где 
– момент инерции тела относительно неподвижной оси вращения,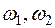 
- начальная и конечная угловые скорости тела.
В случае если центр масс тела движется поступательно со скоростью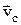 
, а все остальные точки этого тела вращаются вокруг оси, проходящей через центр масс, то можно говорить о плоском движении. Полная кинетическая энергия тела в этом случае: 
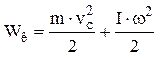, где I – момент инерции тела относительно оси, проходящей через центр масс (точка С), перпендикулярно плоскости чертежа, 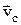- скорость движения центра масс.
Можно показать, что работа упругих сил и сил тяготения не зависит от формы пути, а определяется только начальным и конечным положениями точки приложения силы. Такие силы называются консервативными.
Силы, работа которых не зависит от формы пути, а определяется только координатами начального и конечного положения материальной точки, называются консервативными. Работа консервативных сил по замкнутому пути равна нулю.
Диссипативные силы – это силы, работа которых зависит от формы пути. Работа таких сил по замкнутому пути никогда не равна нулю. Работа силы трения при перемещении по замкнутому пути не равна нулю. Сила трения является неконсервативной – диссипативной.
Если в каждой точке пространства на помещенную туда частицу действует сила, то говорят, что частица находится в поле сил. Например: поле сил тяжести, упругих сил, сил сопротивления и т. д. Если силы, действующие в поле, консервативные, то поле называется потенциальным.
Потенциальная энергия – это энергия, обусловленная конфигурацией тел системы (или частей одного тела). Потенциальная энергия может быть только в системе материальных точек, в которой действуют консервативные силы.
Потенциальная энергия упругого деформированного тела: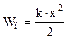 
, где х – величина деформации.
Найдем потенциальную энергию тела в поле тяжести Земли.
Потенциальная энергия зависит от координат. Она может быть положительной и отрицательной, поскольку начальный уровень отсчета потенциальной энергии можно выбрать произвольно.
Если полагать, что потенциальная энергия тела на поверхности Земли равна нулю, то потенциальная энергия в поле тяжести Земли на высоте h от центра Земли (h << RЗ) будет равна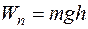 
. На больших расстояниях между Землей и телом использовать эту формулу затруднительно, поскольку ускорение свободного падения изменяется с высотой. На тело, находящееся на высоте h, соизмеримой с радиусом Земли, действует сила 
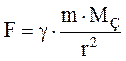, здесь r расстояние от центра Земли до тела. При удалении тела на от поверхности Земли элементарнаяработа силы тяготения: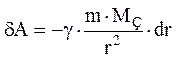 
(«минус», так как сила 
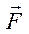и направлены в противоположные стороны).
Если тело переместилось из точки, находящейся на расстоянии r1 в точку, находящуюся на расстоянии r2>r1, то работа силы тяготения 
. Работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус.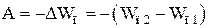 
. Следовательно, 
и потенциальная энергия тела в поле тяготения Земли определяется по формуле: 
. Для удобства принимают потенциальную энергию при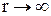 
равной нулю.
В потенциальном поле вводят понятие потенциал: 
. Потенциал поля тяготения: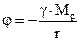 
, где r – расстояние от материальной точки, создающей поле, до рассматриваемой точки поля.
Зная вид функции Wп (x,y,z), можнонайти консервативную силу, действующую на материальную точку в каждой точке силового поля. Рассмотрим перемещение материальной точки вдоль оси х на dx. При этом над материальной точкой совершается работа: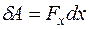 
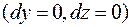. Эта работа равна убыли потенциальной энергии: 
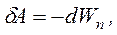следовательно: 
а значит: 
Для проекций силы на оси y и z аналогично, следовательно: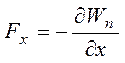 
, 
, 
.
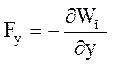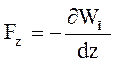Отсюда вектор силы: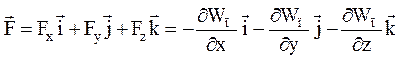 
.
Следовательно: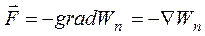 
. Консервативная сила равна градиенту потенциальной энергии, взятому с обратным знаком.
Градиентом скалярной величины называется вектор, характеризующий быстроту изменения этой величины в пространстве. Этот вектор направлен в сторону наиболее быстрого возрастания величины и численно равен скорости этого возрастания.
Основное свойство гравитационного поля: на всякую материальную точку массой m, внесенную в это поле, действует сила тяготения F пропорциональная массе m: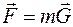 
, где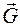 
- напряженность поля тяготения, его силовая характеристика.
Следовательно, для гравитационного поля: 
, 
, 
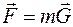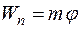. Следовательно: 
. Эта формула говорит о том, что в каждой точке поля тяготения вектор напряженности направлен в сторону наиболее быстрого уменьшения потенциала.
Для замкнутой системы материальных точек, между которыми действуют только консервативные силы, выполняется закон сохранения механической энергии: полная механическая энергия замкнутой системы не меняется с течением времени 
.
Для незамкнутой системы тел изменение полной механической энергии равно работе внешних сил: 
.
Если в системе действуют силы трения, то их работу нужно учитывать также как и работу внешних сил. Поскольку работа сил трения отрицательна, то при наличии сил трения полная механическая энергия убывает (превращается в другие виды энергии).
