 Моментом силы
Моментом силы 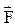 относительно неподвижной точки О, называется векторная физическая величина, равная векторному произведению радиус-вектора
относительно неподвижной точки О, называется векторная физическая величина, равная векторному произведению радиус-вектора  , проведенного из точки О в точку приложения силы, на силу
, проведенного из точки О в точку приложения силы, на силу 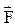 .
.  .
.
Вектор 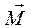 направлен перпендикулярно плоскости, образованной векторами
направлен перпендикулярно плоскости, образованной векторами 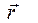 и
и  . Следовательно,
. Следовательно,  и
и  .
.
Модуль момента силы:  , где
, где  - угол между векторами
- угол между векторами  и
и  ,
,  - плечо силы. Плечо силы d – это кратчайшее расстояние от точки О до линии действия силы.
- плечо силы. Плечо силы d – это кратчайшее расстояние от точки О до линии действия силы.
В СИ момент силы измеряется в ньютонах умноженных на метр (Н м).
Моментом силы относительно некоторой оси  , проходящей через точку О, называется проекция Mz на эту ось вектора момента силы
, проходящей через точку О, называется проекция Mz на эту ось вектора момента силы  относительно точки О.
относительно точки О.
 Моментом импульса (моментом количества движения) материальной точки m относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиус-вектора материальной точки, проведенного из точки О, на её импульс:
Моментом импульса (моментом количества движения) материальной точки m относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиус-вектора материальной точки, проведенного из точки О, на её импульс: 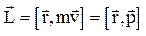 .
.
Направление вектора момента импульса  относительно неподвижной точки О определяется так же, как и для момента силы.
относительно неподвижной точки О определяется так же, как и для момента силы. 
Модуль момента импульса: 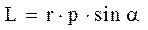 где
где  – угол между векторами
– угол между векторами  и
и 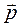 .
.
Момент импульса материальной точки m относительно оси  , проходящей через точку О – это проекция на эту ось вектора момента импульса относительно точки О.
, проходящей через точку О – это проекция на эту ось вектора момента импульса относительно точки О.
Момент импульса системы материальных точек относительно неподвижной точки О равен геометрической сумме моментов импульса относительно той же точки всех материальных точек системы:  .
.
Основной закон динамики твердого тела, вращающегося вокруг неподвижной точки: скорость изменения момента импульса твердого тела относительно неподвижной точки равна сумме моментов всех внешних сил, действующих на тело, относительно этой точки: 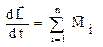 .
.
Основной закон динамики для тела, вращающегося относительно неподвижной оси  : скорость изменения момента импульса тела относительно неподвижной оси вращения равна сумме моментов внешних сил, действующих на тело, относительно той же оси
: скорость изменения момента импульса тела относительно неподвижной оси вращения равна сумме моментов внешних сил, действующих на тело, относительно той же оси  .
.
В случае вращения вокруг неподвижной оси, момент импульса тела можно выразить через угловую скорость вращения  . Здесь I момент инерции твердого тела относительно выбранной оси. Момент инерции тела зависит как от величины массы, так и от распределения массы тела относительно оси вращения. В СИ единицей измерения момента инерции является килограмм, умноженный на метр в квадрате.
. Здесь I момент инерции твердого тела относительно выбранной оси. Момент инерции тела зависит как от величины массы, так и от распределения массы тела относительно оси вращения. В СИ единицей измерения момента инерции является килограмм, умноженный на метр в квадрате.
Тогда основной закон динамики для тела, вращающегося относительно неподвижной оси, можно записать и в другой форме:  . Здесь
. Здесь 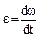 - угловое ускорение.
- угловое ускорение.
Для замкнутой системы момент внешних сил всегда равен нулю, так как по определению, замкнутой называется система, на которую не действуют внешние силы, либо их действие скомпенсировано. Поэтому из основного закона динамики вращательного движения вытекает закон, называемый законом сохранения момента импульса. Момент импульса замкнутой системы относительно неподвижной точки О не изменяется с течением времени:  .
.






