Соответствие между множествами. Понятие функции

Пусть 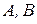– произвольные множества. Декартово произведение множеств и (обозначается как 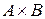) – это множество всех упорядоченных пар 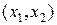таких, что .

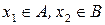Пример 2. При записи шахматной партии используются множества

–для обозначения вертикалей, 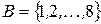–для обозначения горизонталей. Поля шахматной доски обозначаются с помощью элементов множества . ■

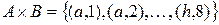Можно построить декартово произведение произвольного числа множеств:

.

Упорядоченный набор элементов 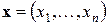будем далее называть вектором. Компоненты 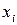будем называть проекциями вектора:

Рассматривая частный случай декартова произведения при 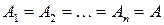, получим множество .

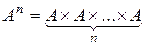Используя понятие декартова произведения, определим соответствие между множествами как упорядоченную тройку множеств:

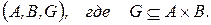(2)

Множество , которое состоит из векторов , называется графиком соответствия. Зададим область определения соответствия как множество

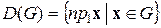
и область значений соответствия как множество

.

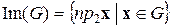Пусть теперь – произвольный фиксированный элемент множества 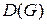. Элемент 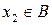называется образом элемента при данном соответствии, если 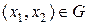. Если при данном соответствии каждый элемент из области определения имеет единственный образ, то соответствие называют функцией.

В дальнейшем изложении встретятся функции многих переменных, то есть функции, для которых множество из (2) само является декартовым произведением: 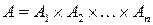. Компоненты 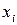вектора являются в этом случае независимыми переменными (аргументами). Обозначать такие функции будем как или .

Пример 3. Расстояние точки на координатной плоскости 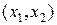от начала координат может быть задано функцией f: R ² → R, которая представлена формулой ■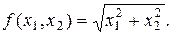