НАЧАЛЬНЫЕ СВЕДЕНИЯ О МНОЖЕСТВАХ И ФУНКЦИЯХ
Понятие о множестве. Операции над множествами
Понятие множество относится к исходным понятиям математики. Оно обозначает набор, совокупность каких-либо объектов, называемых элементами множества. Если элемент 
встречается в наборе, представляющем данное множество 
, говорят, что элемент принадлежит данному множеству: 
.
Если каждый элемент, который принадлежит множеству , принадлежит в то же время множеству 
, то множество называют подмножеством множества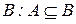 
( включается в ). При работе с подмножествами принято, что для любого множества :
Символ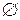 
используется для обозначения пустого множества, то есть множества, которому не принадлежит ни одного элемента. Множество 
называется универсальным, если для любого множества выполняется условие 
. Если выполняются условия 
и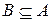 
, говорят, что и – равные множества: 
.
Для задания множества можно использовать следующие способы:
1) перечислить все элементы, принадлежащие множеству;
2) задать порождающую процедуру, которая позволяет определить все элементы искомого множества, совершая действия с элементами уже известного множества;
3) указать универсальное множество и характеристическое свойство, позволяющее выбрать из все те и только те элементы, которые принадлежат искомому множеству.
Перечислением элементов можно задать только конечное множество, то есть множество, содержащее конечное число элементов.
Пример 1. Рассмотрим конечные множества, заданные перечислением элементов:
– множество всех букв латинского алфавита;
– множество всех арабских цифр;
– бинарное множество логических констант. ■
С множествами произвольной природы можно совершать операции объединения и пересечения, определять разность множеств и дополнение множества. Наглядное представление об этих операциях дают диаграммы Венна. На таких диаграммах множества изображаются произвольными фигурами, лежащими в плоскости, соответствующей универсальному множеству . Приведем определения для указанных операций.
Объединением множеств и (обозначается как 
) называется множество всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств , . Символьная запись данного определения:
Пересечением множеств и (обозначается как 
) называется множество всех тех и только тех элементов, которые принадлежат и 
:
Разностью множеств и (обозначается как 
) называется множество всех тех и только тех элементов множества , которые не принадлежат :
Дополнением множества (обозначается как 
, или 
) называется множество всех тех и только тех элементов, которые не принадлежат :
.
Иллюстрации данных операций в виде диаграмм Венна приведены на рис.1-4.
В заключение приведем некоторые тождества теории множеств:
(1)
