Основные положения

Лабораторные работы № 16а, 16б

 

Изучение затопленной свободной турбулентной струи

Основные положения

Турбулентная струя называется свободной и затопленной, если она распространяется в безграничном пространстве, заполненном неподвижной средой с теми же физическими свойствами, что и вещество среды (рис. I).

 

 

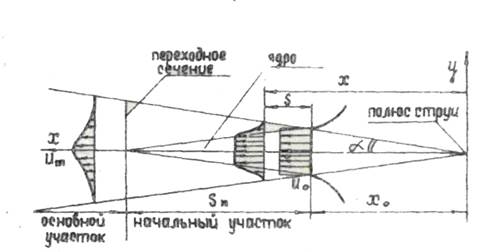
Рис. I. Схема свободной затопленной турбулентной струи

 

На выходе из сопла частицы струи имеют одинаковую скорость» направленную вдоль оси струи. По мере удаления от сопла струя вовлекает в свое движение ранее неподвижные массы окружающей жидкости. Вблизи границы струи возникает турбулентный погранич­ный слой, толщина которого по направлению распространения струи увеличивается за счет расширения самой струи и уменьшения ядра, в котором частицы жидкости имеют скорость истечения uо. В пограничном слое за счет турбулентного перемешивания и подсоса внеш­ней жидкости продольная скорость частиц струи и. уменьшается, и появляется поперечная составляющая скорости V. В пределах пограничного слоя продольная составляющая скорости уменьшается от u0 на границе с ядром до 0 на границе струи. Поперечная ско­рость на границе струи не равна 0, т.к. через границу происходит подсос окружающей годности. Однако везде, кроме области вблизи самой границы струи, поперечная скорость мала по сравнению с продольной. В дальнейшем под скоростью струи в данной точке бу­дем подразумевать продольную составляющую скорости u.

В некотором сечении струи, называемом переходным, невозмущённое ядро потока исчезает. Участок струи, расположенный между

 

срезом сопла и переходным сечением, называется начальным. Участок струи, следующий за начальным, называется основным. В основном участке струи происходит уменьшение скорости на оси струи u_m. (максимальной в данном сечении) и тем больше, чем дальше находится сечение от среза сопла, в то время как в пределах всего началь­ного участка скорость на оси u_m = u₀.

На основании экспериментального исследования установлено:

1) Профиль скорости в основном участке струи - универсальный, это
значит, что если в двух сечениях струи выбрать точки, отстоящие
от оси струи на расстоянии y₁ и y₂, причем

/I/

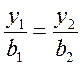
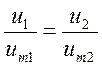то,,

 

где 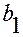, 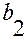- ширина струи, а 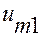, 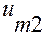- скорости на оси струи в сечениях I и 2.

 

2) Границы струи прямолинейны. В пределах основного участка поток жидкости ведёт себя так, как будто струя создана точечным турбулентным источником, помещённым в месте пересечения границ струи / в полюсе струи / (рис.I). Для круглой струи полюс представляет из себя точку, для плоской – линию. Тогда ширина струи

/2/

,

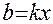где x – расстояние вдоль струи, отсчитываемое от полюса,

k – постоянная. Тогда, из /1/ и /2/ следует, что

/3/

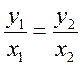
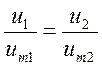, если

 

/4/

Следовательно, .

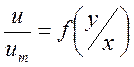Линии разных скоростей /изотахи/ представляет из себя прямые линии, выходящии из полюса. Выберем значения yt в каждом сечении, для которого u(yt)=tum1, 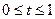- некоторое произвольное число. Тогда в двух сечения согласно /1/

	/5/

 

 

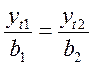
Значит отношение скорости u1 u2, в любых точках этих сечений к осевой из /1/ и /5/:

/6/

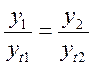
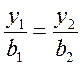, если

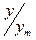
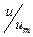Поэтому, если построить график зависимости от (чаще всего t=1/2),

то для любого сечения в пределах нового участка профили скорости будут укладываться на одну кривую.

Такое построение является доказательством универсальности профиля

 

3). Давление в струе постоянное и равно давлению в окружающей среде.

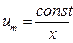Тогда из теоремы импульсов следует постоянство количества движения струи в любом сечении. На основание этого можно доказать [I], что в пределах основного участка для круглой струи

/7/

,

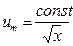
для плоской струи.

 

 

На основании этих фактов можно считать, что в основном участке плоской и круглой турбулентной струи поток создан источником, расположенном в полюсе струи. Закономерности развития течения в основном участке можно найти из решения задачи о турбулентном истечении жидкости из источника, представляющего из себя точку (круглая струя) или линию (плоская).

Обе задачи решены на основании полуэмпирической теории турбулентности и уравнений пограничного слоя с учётом универсальности скорости /4/ и измерения осевой скорости /7/. Для напряжения турбулентного трения применяется формула Прандтля.

 

	/8/

 

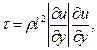
где ρ – плотность жидкости. Для пути смещения l предполагается линейная зависимость

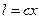
. Постоянная с является единственной эмпирической величиной теории, определяемой из опыта. В дальнейшем удобно использовать другую постоянную

.

 

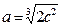Постоянная a называется коэффициентом струи. При обычных условиях для круглой струи 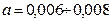, для плоской .

 

/9/

Универсальный профиль для безразмерной скорости круглой струи из решения имеет вид

,

 

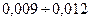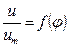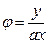
Универсальный профиль скорости [2]

для круглой струи

Таблица 1

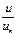
	0.0	0,2	0,4	0,5	0,6	0,8	1.0
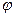
	3,40	1,99	1,45	1,25	1,01	0,59	0,00

 

 

Из решения также следует, что 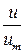< 0.5a в пределах струи.

Поэтому продольная составляющая скорости существенно больше поперечной составляющей скорости v везде, кроме области вблизи границы струи. Если β – угол наклона изотахи к оси струи, для точек которой 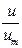= t, то

/10/

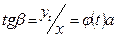
Отсюда угол раскрытия круглой струи (на границе струи u=0)

/11/

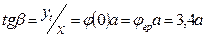
Используя /9/, можно получить [I] значение константы в /7/.

/12/

Для круглой струи ,

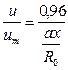где Ro-радиус сопла. Если S-расстояние до данного сечения струи от среза сопла, то

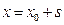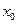, / - расстояние от полюса до среза сопла/, (рис.I). Тогда,

/13/

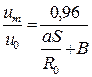
где 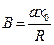- постоянная, определяющая положение полюса. Значение этой постоянной также как и значение a определяется из опыта.

Обычно значение B находят из условия, что угол раскрытия струи α в начальном и основном участке струи совпадают /как это показано на рис.I/. Из этого следует, что граница струи, истекающей из полюса, проходит через кромки сопла: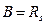

при 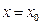/ s=0 /. Тогда

/14/

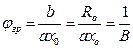
или 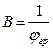. Для круглой струи 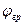=3.4, B=0.29

 

Для этого значения B положение полюса

	/15/

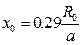
положение переходного сечения получим из /12/, если положить

/16/

;

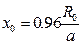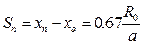
По формулам /11/,/13/,/15/,/16/ при B=0.29, производят приближённый расчёт круглой свободной затопленной турбулентной струи.

 

Цель работы

 

1. Убедиться в универсальности профиля скоростей в основном участке струи.
2. Определить коэффициент структуры струи a и полюсное расстояние

 

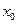
Описание лабораторной установки

 

Установка состоит из центробежного вентилятора 1 со всасывающим

3 и нагнетательным 4 трубопроводами /рис.2/. Струя образуется при истечении из профилированного сопла 5 с диаметром с диаметром выходного отверстия 60 мм.

Для выравнивания профиля скорости перед соплом внутри напорного трубопровода установлена набивка из медных трубок небольшого диаметра. Измерение скорости производится с помощью трубки Прандтля 6, укреплённой на координатнике 7, и микроманометре ММН 8.

С помощью координатника 7 можно фиксировать положение трубки Прандтля

в трёх измерениях 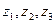/рис. 2./. Профиль скорости измеряется с помощью перемещения трубки в вертикальной плоскости вдоль оси 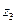. Вследствие симметрии струи, эти измерения можно проводить в любой плоскости, проходящей через ось струи.

Перемещая координатник вдоль оси 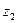переходим от одного сечения к другому.

Координату 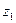не меняют во времени измерений, перемещая трубку только в вертикальной плоскости, проходящей через ось струи.

 

 

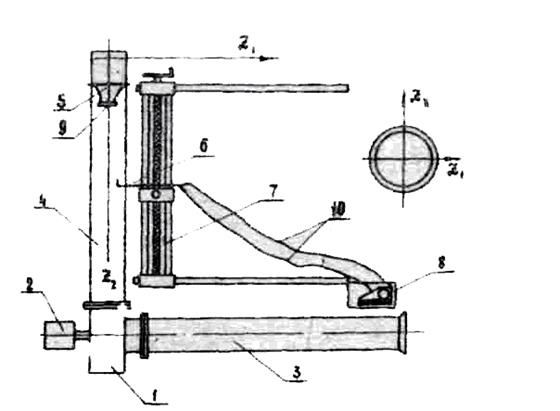
Рис. 2. Схема установки:

1 – вентилятор, 2 – электродвигатель, 3 – всасывающий трубопровод, 4 – нагнетательный трубопровод, 7 – сопло, 8 – микроманометр, 9 – крышка, 10 – резиновые трубки.