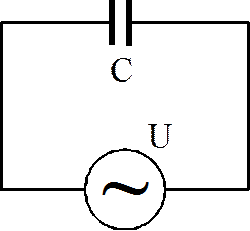 |
Схема цепи с конденсатором изображена на рис.6.
Как известно, ёмкость конденсатора определяется соотношением
С = Q/U (13)
где Q – заряд на пластинах конденсатора,
U - разность потенциалов между пластинами.
Ёмкость показывает, какой заряд необходимо сообщить пластинам конденсатора, чтобы изменить разность потенциалов между ними на единицу.
Ёмкость конденсатора определяется формой и размерами пластин (обкладок), величиной зазора между ними и свойствами заполняющего конденсатор диэлектрика. Для плоского конденсатора ёмкость равна
C =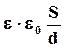 
,
где e- диэлектрическая постоянная среды между обкладками,
S - площадь перекрытия пластин (обкладок),
d - расстояние между пластинами,
e0- постоянная вакуума, равная 8,85.10-12 ф/м (в СИ).
Рассмотрим процессы, происходящие в цепи с конденсатором. Если к цепи приложено внешнее напряжение U(t) = Uо.sin wt, то под действием этого напряжения конденсатор будет периодически заряжаться и разряжаться.
Напряжение между обкладками конденсатора в соответствии с (13) будет равно
UC = Q/C
Заряд на обкладках конденсатора можно найти исходя из определения силы тока. Так как сила переменного тока равна I = dQ/dt, то заряд будет равен
Q =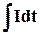 
.
Следовательно, величина напряжения между обкладками конденсатора будет равна
UC=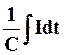 
Для нахождения силы тока в цепи воспользуемся опять правилом Кирхгофа. В данном случае роль падения напряжения играет напряжение на конденсаторе, а роль ЭДС – проложенное напряжение. Поэтому, по правилу Кирхгофа для данной цепи получим
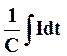= Uо.sinwt.
Продифференцировав данное выражение, получим
I(t) = Cw·U0 cos wt
Пользуясь тригонометрическими формулами преобразуем полученное соотношение к виду:
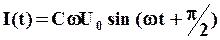(14)
Сравнивая выражения для тока и напряжения, видим, что в цепи с конденсатором ток и напряжение изменяются не в фазе. Ток опережает напряжение на 90o или на четверть периода (Т/4). Выражение (14) позволяет найти связь между амплитудой внешнего напряжения Uо и амплитудой тока Iо для цепи, содержащей конденсатор.
Произведение UоwC, входящее в выражение для тока, очевидно, имеет смысл амплитуды тока Iо.
Iо = UоwC =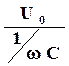 
(15)
Соотношение (15) напоминает закон Ома для постоянного тока. Величина 1/wC играет роль сопротивления в цепях, содержащих конденсатор. Эту величину называют ёмкостным сопротивлением цепи ХС.
XС = 1/wC = 1/(2pfC). (16)
Как следует из (16), ёмкостное сопротивление ХС зависит от частоты. С ростом частоты ёмкостное сопротивление уменьшается. Для постоянного тока (f = 0) ёмкость обладает бесконечно большим сопротивлением, и ток в такой цепи протекать не будет.
Так же как омическое и индуктивное сопротивления, емкостное сопротивление измеряется в Омах. Следует отметить, что и при ёмкостном сопротивлении происходит периодическое накопление энергию в виде энергии электрического поля, а затем возвращение её источнику. По этой причине ёмкостное сопротивления, как и индуктивное, является реактивным сопротивлением.
