Рассмотрим операции для регулярных языков. Пусть есть два языка L и M, где LÍ∑* и МÍ∑*-подмн-ва одного и того же алфавита, но если LÍ∑L и МÍ∑М, то можно сказать что ∑=(∑LÈ∑М), т.е. деделаем новый алфавит, в котором эти два языка.
LÈM-объединение-мн-во всех цепочек принадлежащих L или М.
LÇM-пересечение-мн-во всех цепочек, принадлежащих и L, и М.
L-M-мн-во всех цепочек, принадлежащих L, одновременно не принадлежащих М.
Ḹ=∑*-L- дополнение
Теорема: LÈM-регулярный язык для регулярных языков L и М, т.е. L=L(R), M=L(S), где L(R) и M(S) –регулярные выражения от языков R и S, тогда LÈM=L(R+S).
Если L-регулярный язык, то Ḹ-тоже. Т.е. есть такой конечный автомат допускающий цепочки из L. Все допускающие состояния объявим, как недопускающие, а недопускающие преобразуем в допускающие.
Пересечение всех цепочек тоже является регулярным языком: 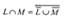
Обращение цепочки-это цепочка выписанная в обратном порядке:
w=a1…an
wR=an…a1
Тогда если L-регулярный язык, то LR-тоже. LR={wR|wÎL}
Гомоморфизм цепочки-ф-ция на мн-ве цепочек, которая вместо каждого символа цепочки подставляет другую цепочку, т.е. есть некоторое отображение h, которое каждому символу алфавита ставит в соответствие цепочку h:∑→∑*
w=a1…an
h(w)=h(a1)h(a2)…h(an)
h(L)={V|V=h(w), wÎL}
Теорема: если L-регулярный язык, то h(L) также.
Обратный гомоморфизм также сохраняет регулярность языков, т.е. если h:∑→Т и L-регулярный язык над Т, то h(L)-регулярный язык от ∑.
Деревья разбора.
Дерево разбора для грамматики G это дерево, обладающее след. свойствами: каждая внутренняя вершина дерева помечена переменной из N. Каждый лист отличен либо переменной либо терминалом либо e(пустой строкой), причем вершина e должна быть единственным наследником у своего родителя. Если вершина А-внутренняя вершина, а его сыновья слева направо x1,x2,…,xn, то значит существует продукция вида A→ x1,x2,…,xn.
Листья любого дерева разбора при их просмотре слева направо образуют цепочку которая называется кроной дерева. Кроной дерева разбора яв-ся выводимая цепочка.
Равносильно след. утверждение: 1) процедура рекурсивного вывода определяет, что цепочка принадлежит языку переменной А; 2) A=>w; 3) A =>L w; 4)A =>R w; 5) существует дерево разбора с корнем А и кроной w.
Нормальная форма Хомского контекстно-свободных грамматик.
Покажем, что каждый КС-язык, не содержащий пустой цепочки, порождается грамматикой, все продукции которой имеют вид: А→ВС, А→а, где большие буквы-переменные, а малые-терминал.
Представление грамматики в таком виде называется нормальной формой Хомского. Для приведения грамматики к такому виду необходимо: 1) удалить бесполезные символы, т.е. все переменные и терминалы, которые не встречаются порождением терминала цепочек из стартового символа; 2) удалить продукции вида А→e, т.е. порождения пустых цепочек; 3) удалить цепные продукции вида А→В, где А и В-переменные.






