В общем случае для любого НКА можно построить ДК с количеством состояний zn, где n-количество состояний недетерминированного конечного автомата.
AN={QN, ƩN, δN, q0N, FN}; AD={QD, ƩD, δD, q0D, FD}; L(AN)=L(AD)
1) Алфавит ƩN и ƩD – совпадают
2) QD ⊆ 2QN, причем, если какое-то множество состояний недопустимо в НКА, то оно не входит в QD.
3) F – множество всех подмножеств, таких, что в пересечении с FN оно не пусто.
4) Для каждого подмн. мн. символов S ≤ QN и входного символа a δs(a,s)= 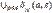
| A B C D | |||
| →q0 q1 * q2 q0q1 * q0q2 * q1q2 * q0q1q2 | q0q1 ∅ q2 q0q1 q0q1q2 q2 q0q1q2 | q0 q2 q2 q0q2 q0q2 q2 q0q2 |
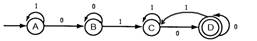
При построении ДКА в качестве начального, используется состояние, соответствующее мн. {q0}. Данное состояние является достижимым.
Пусть S – мн. достижимых состояний, тогда мн. состояний SU{S’(δD(S,Q)=S’, S ∈δ, a ∈ Ʃ}. Теорема: Если ДКА D={QD, ƩD, δD, {q0}, FD} построен из N={QN, Ʃ, δN, q0, FN} методом конструкции подмножеств, то их языки совпадают L(D)=L(N).
Теорема2: Язык L допустим некоторым ДКА тогда и только тогда, коггда допустим некоторый НКА.
Алгоритм преобразования НКА а ДКА: 1) Пусть q0 – нач. состояние НКА, тогда { q0} – нач. сост. ДКА. Пусть Р – состояние НКА, в которое можно попасть из q0 по значениям входных символов q1, q2,…, qn, тогда состояния { q0, r1, …, rk, p} являются сост. ДКА, где, r1, …, rk – это все состояния, в которые можно попасть из q0 по любому суффиксу входного слова.
Конечные автоматы с эпсилон-переходами.
Это пятерка вида E=(Q, Ʃ, δ, q0, F).
δ, Ʃ U [Ɛ]xQ→Q
Пример: автомат, который имеет вещественные числа:

| Ɛ | 0..9 | . | +,- | |
| →q1 q2 q3 q4 q5 | q2 ∅ q5 q5 ∅ | q0∅ q2,q3 ∅ q4 ∅ | ∅ q4 q4 ∅ ∅ | q2 ∅ ∅ ∅ ∅ |
Эпсилон-замыкание некоторого НКА все состояния, по которым можно поспасть из заданного по Ɛ-переходу. ECLOSE(q) содержит состояние q.
Определим расширенную функцию переходов: δ^(w,q0), δ^(Ɛ,q)=Ɛ(q); Язык: L(E)={w|δ^(w,q0) ⋂F=∅}; Теорема: язык Lдопускается неким Ɛ-НКА тогда и только тогда, когда он допускается неким ДКА.
Регулярные выражения.
1) Объединение двух языков L и M, обозначаемое L ∪ M – это множество цепочек, которые содержатся либо в L, либо в M, либо в обоих языках. Например, если L = {001, 10, 111} и M={Ɛ, 001}, то L ∪ M = {Ɛ, 10, 001, 111}.
2) Конкатенация языков L и M – это мн. цепочек, которые можно образовать путем дописывания к любой цепочке из L любой цепочки из M. например, если L = {001, 10, 111} и M={Ɛ, 001}, то LM – это {001, 10, 111, 001001, 10001, 111001}
3) Итерация языка L обозначается L* и представляет собой мн. всех тех цепочек, которые можно образовать путём конкатенации любого количества цепочек из L. L* можно представить как бесконечное объединение  , где L0={Ɛ}, L1=L и Li для I > 1 равен LL..L (конкатенация i копий L).
, где L0={Ɛ}, L1=L и Li для I > 1 равен LL..L (конкатенация i копий L).
Определим методы построения регулярных выражений.
Константы Ɛ и ∅ являются регулярными выражениями, определяющими языки { Ɛ } и ∅, соответственно, т.е. L{Ɛ}={Ɛ} и L{∅}={∅}.
Если a – произвольный символ, то а – регулярное выражение, определяющее язык {а}, т.е. L(a)={a}.
Переменныя, обозначенная прописной курсивной буквой, например, L, представляет произвольный язык.
Пусть E и F – регулярные выражения, тогда
1) E + F – регулярное выражение, определяющее объединение языков L(E) и L(F), т.е. L(E + F)=L(E) ∪L(F).
2) EF – регулярное выражение, определяющее конкатенацию языков языков L(E) и L(F). Таким образом, L(EF)=L(E)L(F).
3) E* - регулярное выражение, определяющее итерацию языка L(E), таким образом, L(E*)=(L(E))*.
4) (E) – регулярное выражение, определяющее тот же язык L(E), что и выражение E, т.е. L((E))=L(E)
Приоритет операций:
1) *; 2) конкатенация; 3) объединение (+)






