1. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид …
a) (11; 12,1)
b) (9,8; 11)
c) (9,8; 10,8)
d) (10,1; 11,9)
2. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид …
a) (10,8; 12)
b) (10,6; 13,4)
c) (11,2; 11,8)
d) (12; 13,7)
3. Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид …
a) (11,8; 12,8)
b) (13; 14,6)
c) (11,6; 13)
d) (11,8; 14,2)
4. Точечная оценка математического ожидания нормального распределения равна 14. Тогда его интервальная оценка может иметь вид …
a) (12,6; 15,4)
b) (14; 15,1)
c) (12,1; 14)
d) (12,7; 13,7)
5. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид...
a) (11; 11,5)
b) (10,5; 10,9)
c) (10,5; 11,5)
d) (10,5; 11)
6. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид...
a) (12; 12,6)
b) (11,4; 11,5)
c) (11,4; 12)
d) (11,4; 12,6)
7. Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид...
a) (13; 13,7)
b) (12,3; 12,8)
c) (12,3; 13,7)
d) (12,3; 13)
8. Точечная оценка математического ожидания нормального распределения равна 14. Тогда его интервальная оценка может иметь вид...
a) (12,5; 13,4)
b) (12,5; 14)
c) (14; 15,5)
d) (12,5; 15,5)
9. Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид...
a) (13,8; 14,1)
b) (13,8; 15)
c) (15; 16,2)
d) (13,8; 16,2)
10. Точечная оценка математического ожидания нормального распределения равна 16. Тогда его интервальная оценка может иметь вид...
a) (14,9; 16)
b) (16; 17,1)
c) (14,9; 17,1)
d) (14,9; 15,2)
Интерполирование функций_ многочлены второго порядка
1. График функции 
проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a) 
b)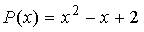 
c) 
d)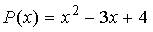 
2. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a)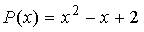
b)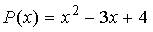
c)
d)
3. График функции проходит через точки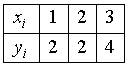 
Тогда ее интерполяционный многочлен второго порядка равен…
a)
b)
c)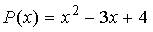
d)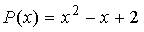
4. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a)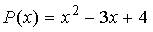
b)
c)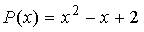
d)
5. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a) 
b) 
c) 
d) 
6. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a)
b)
c)
d)
7. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a)
b)
c)
d)
8. График функции проходит через точки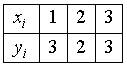 
Тогда ее интерполяционный многочлен второго порядка равен…
a)
b)
c)
d)
9. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a) 
b) 
c) 
d) 
10. График функции проходит через точки 
Тогда ее интерполяционный многочлен второго порядка равен…
a)
b)
c)
d)
