1. График функции 
изображен на рисунке.
Тогда значение производной этой функции в точке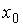 
равно ….
a) 0,5
b) 1
c) 
d) – 1
2. График функции изображен на рисунке.
Тогда значение производной этой функции в точке 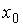равно ….
a)
b)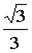 
c) 
d)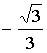 
3. График функции изображен на рисунке.
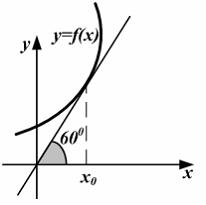
Тогда значение производной этой функции в точке 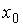равно ….
a)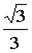
b)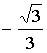
c)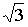 
d)
4. График функции изображен на рисунке.
Тогда значение производной этой функции в точке 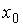равно ….
a) 0,5
b)
c) 1
d) – 1
5. График функции изображен на рисунке.
Тогда значение производной этой функции в точке 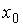равно ….
a)
b)
c)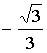
d)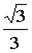
6. График функции изображен на рисунке.
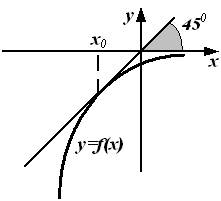
Тогда значение производной этой функции в точке 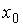равно ….
a) 1
b) – 1
c)
d) 0,5
7. График функции изображен на рисунке.
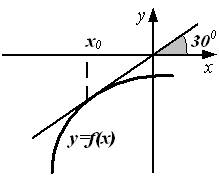
Тогда значение производной этой функции в точке 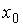равно ….
a)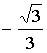
b)
c)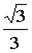
d)
8. График функции изображен на рисунке.
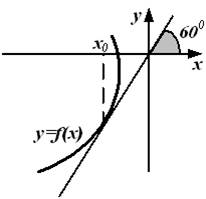
Тогда значение производной этой функции в точке 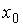равно ….
a)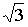
b)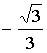
c)
d)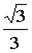
9. График функции изображен на рисунке.
Тогда значение производной этой функции в точке 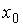равно ….
a) 1
b) – 1
c)
d) 0,5
10. График функции изображен на рисунке.
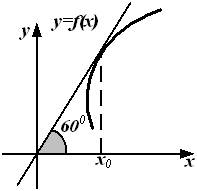
Тогда значение производной этой функции в точке 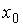равно ….
a)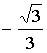
b)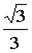
c)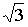
d)
Градиент скалярного поля
1. Градиент скалярного поля 
в точке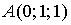 
имеет вид…
a)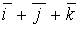 
b)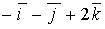 
c) 
d) 
2. Градиент скалярного поля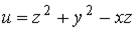 
в точке 
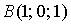имеет вид…
a)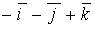 
b)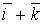 
c)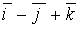 
d) 
3. Градиент скалярного поля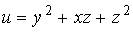 
в точке 
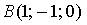имеет вид…
a)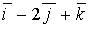 
b)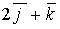 
c)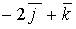 
d)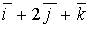 
4. Градиент скалярного поля 
в точке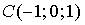 
имеет вид…
a)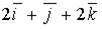 
b) 
c)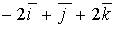 
d) 
5. Градиент скалярного поля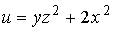 
в точке 
имеет вид…
a)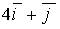 
b)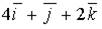 
c) 
d)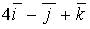 
6. Градиент скалярного поля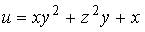 
в точке 
имеет вид…
a)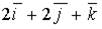 
b)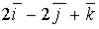 
c) 
d)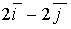 
7. Градиент скалярного поля 
в точке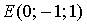 
имеет вид…
a)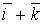
b)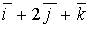
c)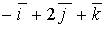 
d)
8. Градиент скалярного поля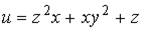 
в точке 
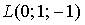имеет вид…
a)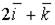 
b)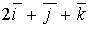 
c) 
d)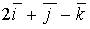 
9. Градиент скалярного поля 
в точке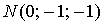 
имеет вид…
a)
b)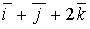 
c)
d)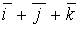
10. Градиент скалярного поля 
в точке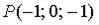 
имеет вид…
a)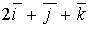
b)
c)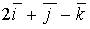
d)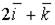
11. Градиент скалярного поля 
в точке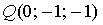 
имеет вид…
a)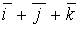
b)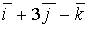 
c)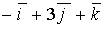 
d)
12. Градиент скалярного поля 
в точке 
имеет вид…
a)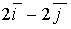
b)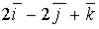
c)
d)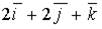
13. Градиент скалярного поля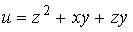 
в точке 
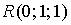имеет вид…
a)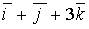 
b)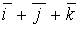
c)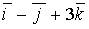 
d)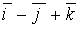
14. Градиент скалярного поля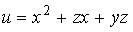 
в точке 
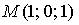имеет вид…
a)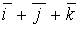
b) 
c) 
d)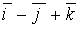
15. Градиент скалярного поля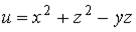 
в точке 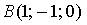имеет вид…
a)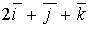
b)
c)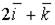
d)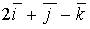
16. Градиент скалярного поля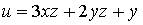 
в точке 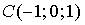имеет вид…
a)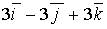 
b)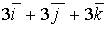 
c)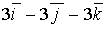 
d)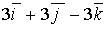 
17. Градиент скалярного поля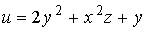 
в точке 
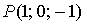имеет вид…
a)
b)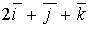
c)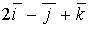 
d)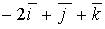 
18. Градиент скалярного поля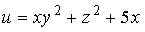 
в точке 
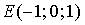имеет вид…
a) 
b) 
c)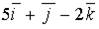 
d)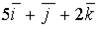 
19. Градиент скалярного поля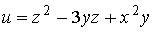 
в точке 
имеет вид…
a)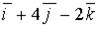 
b) 
c)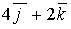 
d)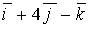 
Двойной интеграл_ геометрический смысл (произвольная область)
1. Пусть 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) прямоугольная трапеция
b) треугольник
c) ромб
d) произвольная трапеция
2. Пусть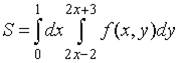 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) параллелограмм
b) ромб
c) произвольная трапеция
d) треугольник
3. Пусть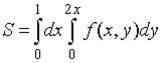 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) произвольная трапеция
b) треугольник
c) параллелограмм
d) ромб
4. Пусть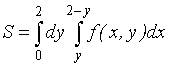 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) ромб
b) треугольник
c) произвольная трапеция
d) параллелограмм
5. Пусть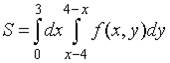 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) треугольник
b) равнобокая трапеция
c) параллелограмм
d) ромб
6. Пусть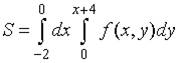 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) трапеция
b) параллелограмм
c) треугольник
d) ромб
7. Пусть 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) трапеция
b) ромб
c) параллелограмм
d) треугольник
8. Пусть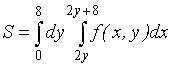 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) ромб
b) трапеция
c) треугольник
d) параллелограмм
9. Пусть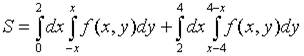 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) параллелограмм
b) ромб
c) треугольник
d) трапеция
10. Пусть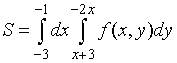 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) трапеция
b) параллелограмм
c) ромб
d) треугольник
Двойной интеграл_ геометрический смысл (прямоугольная область)
1. Пусть 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) треугольник
b) прямоугольник, у которого все стороны равны
c) окружность с радиусом 2
d) прямоугольник
2. Пусть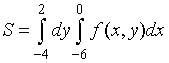 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) треугольник
b) прямоугольник
c) окружность с радиусом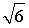 
d) прямоугольник, у которого все стороны равны
3. Пусть 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) окружность с радиусом 2
b) прямоугольник
c) прямоугольник, у которого все стороны равны
d) треугольник
4. Пусть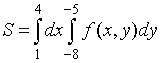 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) прямоугольник, у которого все стороны равны
b) прямоугольник
c) треугольник
d) окружность с радиусом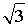 
5. Пусть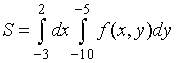 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) окружность с радиусом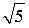 
b) прямоугольник
c) прямоугольник, у которого все стороны равны
d) треугольник
6. Пусть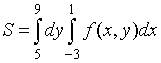 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) прямоугольник
b) треугольник
c) окружность с радиусом 2
d) прямоугольник, у которого все стороны равны
7. Пусть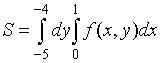 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) окружность с радиусом 1
b) прямоугольник, у которого все стороны равны
c) прямоугольник
d) треугольник
8. Пусть 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) прямоугольник, у которого все стороны равны
b) прямоугольник
c) треугольник
d) окружность с радиусом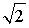 
9. Пусть 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) прямоугольник, у которого все стороны равны
b) окружность с радиусом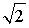
c) треугольник
d) прямоугольник
10. Пусть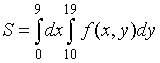 
. Тогда область D, площадь которой выражается данным интегралом, имеет вид…
a) прямоугольник
b) треугольник
c) окружность с радиусом 3
d) прямоугольник, у которого все стороны равны
