имеет вид
Доказательство:
, 
, 
и 
;
.
Понятие о центральной предельной теореме
Это ряд теорем, посвященных выяснению условий, при которых возникает нормальный закон распределения. Ляпунов показал, что в случае, когда СВ Х может быть представлена в виде суммы большого числа независимых в совокупности CВ, каждая из которых вносит незначительный вклад, то СВ распределена по нормальному закону.
.
Показательное распределение
Описывается плотностью распределения 
Найдем функцию распределения
Пусть Т - случайная величина, описываемая по показательному распределению, которое дает время безотказной работы прибора. Тогда 
характеризует среднее число отказов в единицу времени.
.
Пусть 
- гарантийное время работы прибора. Найти вероятность того, что прибор проработает гарантийный срок.
функция надежности для показательного распределения, т.к. она равна вероятности, что прибор проработает время 
.
- характеристический признак именно показательного распределения
Пример2.14. Среднеевремя устранения повреждения канала 
мин. Соответствующее СВ Т описывается показательным распределением. Найти вероятность того, что на восстановление канала потребуется а)более 10 мин; б) от 5 до 10 мин.
Решение:
а) 
мин.
мин.
; 
.
.
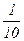б) 
.
Закон больших чисел
В случаях большого числа испытаний или СВ, являющихся суммами большого числа СВ имеет свойство устойчивости средних. Случайное отклонение СВ от среднего в каждом испытании при большом числе испытаний взаимно погашаются, и средний результат может предсказать с большой степенью точности. Устойчивость средних – физическое содержание закон больших чисел.
Теория вероятностей под законом больших чисел понимает ряд теорем, в которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым постоянным величинам. В частности теорема Чебышева дает наиболее общий случай закона больших чисел, а теореме Бернулли – простейший.
Теорема Чебышева
Если СВ 
попарно независимы и их дисперсии ограничены сверху некоторыми константами С, то
Частный случай теоремы Чебышева
Пусть все математические ожидания 
, 
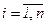то теорема Чебышева запишется в виде:
.
На это формуле основывается выборочный метод математической статистики. По сравнительно небольшой выборке, произведенной случайным образом, можно судить обо всей совокупности исследуемых объектов.
Теорема Бернулли
Если в каждом из n испытаний вероятность события постоянна, то, как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по модулю (абсолютной величине) будет сколь угодно малым, если n достаточно велико.
Замечания
1. По теореме Бернулли в отдельных сериях опытов возможно отклонение относительной частоты от вероятности по модулю больше чем на 
, но при больших 
такое событие маловероятно.
2. В обычном понимании предела последовательности 
подразумевается, что для сколь угодно малой величины существуют такое 
, что для всех 
выполняется неравенство 
. Для приведенного в теореме Бернулли предела это не так, поэтому не говорят, что относительная частота сходится к вероятности, а говорят, что относительная частота сходится к вероятности по вероятности.
