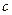
| 
|
|
1. 
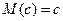
2. 
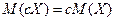
| X | 
| 
| … | 
|
|
| 
| 
| … | 
|
| CX | 
| 
| … | 
|
|
|
|
| … |
|
3. Для независимых СВ 
, 
математическое ожидание 
|
|
|
| … |
|
|
|
|
| … |
|
| 
| 
| … | 
|
|
|
|
| … | 
|
| 
| 
| … | 
| 
| 
| … | 
| … | 
| ||
|
| 
| 
| … | 
| 
| 
| … | 
| … | 
|
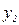
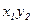
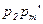
4. Аналогично можно доказать, что 
(независимость не нужна)
5. 
(следует из свойств 2,4)
6. Отклонением называется разность между СВ и ее математическим ожиданием: 
.
.
Пример 2.7. Найти 
, где - число появлений события в 
испытаниях, протекающих в одинаковых условиях.
Решение:
, где -число появления события в одном i-ом испытании.
; 
.
Дисперсия
В качестве характеристики рассеяния нельзя использовать отклонение, т.к. его математическое ожидание равно нулю. Из двух вариантов (и) выбора модуля отклонения 
и квадрата отклонения 
предпочтительней выбрать последний вариант.
Дисперсией СВ называется математическое ожидание квадрата отклонения данной СВ от ее математического ожидания.
Пример 2.8. Найти дисперсию СВ, заданной таблицей
|
| |||
|
| 0,2 | 0,2 | 0,6 |
Решение:
Составим ряд распределения для СВ Х2.
| |||
|
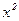
| 0,2 | 0,2 | 0,6 |
,
.
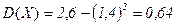Свойства дисперсии
-
. -
/
.
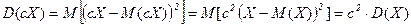Если 
, разброс СВ cX больше.
Если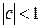 
, разброс СВ cX меньше.
3. Для независимых и 
.
-
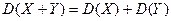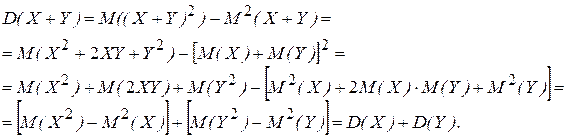
(с- постоянная). -
.
Пример 2.9. Вычислить 
, если – число появления события в испытаниях.
Решение:
Найдем сначала для одного испытания
| ||
|
| 1-р | р |
; 
;
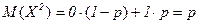Для испытаний
; 
(
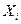- независимые)
Недостаток : ее размерность равна квадрату размерности СВ и ее математического ожидания. Поэтому вводят еще одну характеристику рассеяния.
Среднеквадратическое отклонение
, 
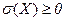
Свойство 
: для взаимно независимых СВ
Другие числовые характеристики смотри ниже.
Непрерывные CB
Пусть CВ Х может принимать любое значение на отрезке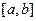 
. Такие CВ могут иметь либо непрерывную либо разрывную функцию распределения вероятностей 
. В дальнейшем под непрерывнойCВ будем понимать такую непрерывную CВ, которая имеет непрерывную функцию распределения.
Для непрерывных CВ функция распределения вероятностей обладает такими же свойствами, что и для дискретных. Кроме того, она обладает дополнительными свойством: вероятность того, что примет одно определенное значение равна нулю 
.
Доказательство:
.
Следует обратить внимание на то, что
· если событие А невозможно, то 
;
· если 
,то из этого не следует, что событие А невозможное.
Плотность распределения вероятности непрерывной CВ (Дифференциальная функция распределения)
Плотностью распределения вероятности непрерывной CВ называют первую производную функции распределения вероятностей
.
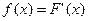Из этого определения следует, что является одной из первообразных 
.
Свойства :
1. Т.к. неубывающая функция, то 
.
