Цель работы: научиться выполнять прогнозирование экономических
параметров с помощью одномерного и многомерного
регрессионного анализа
Содержание работы:
1 Линейный регрессионный анализ.
2 Экспоненциальный регрессионный анализ.
3 Линейный многомерный регрессионный анализ
Линейный регрессионный анализ
Одним из методов, используемых для прогнозирования, является регрессионный анализ.
Регрессия - это статистический метод, который позволяет найти уравнение, наилучшим образом описывающее совокупность данных, заданных таблицей.
| х | x1 | x2 | ... | хi | ... | хn |
| y | x1 | y2 | ... | yi | ... | yn |
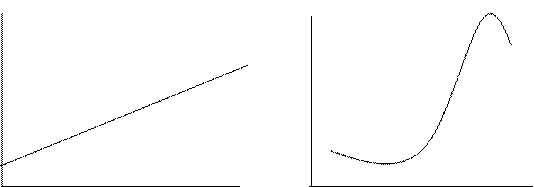На графике эти данные отображаются точками. Регрессия позволяет подобрать к этим точкам кривую у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к табличным данным.
•
у у •
• •
•
• •
• • • •
b • •
Х х
Рисунок 1 Линейная регрессия Рисунок 2 Нелинейная регрессия
По полученному уравнению можно вычислить (сделать прогноз) значение функции у для любого значения х, как внутри интервала изменения х из таблицы(интерполяция), так и вне его (экстраполяция).
Линейная регрессия
Линейная регрессия дает возможность наилучшим образом провести прямую линию через точки одномерного массива данных. Уравнение с одной независимой переменной, описывающее прямую линию, имеет вид:
y=mx+b, (1)
где:
х - независимая переменная;
у -зависимая переменная;
m – характеристика наклона прямой;
b - точка пересечения прямой с осью у.
Например, имея данные о реализации товаров за год с помощью линейной регрессии можно получить коэффициенты прямой (1) и, предполагая дальнейший линейный рост, получить прогноз реализации на следующий год.
Экспоненциальный регрессионный анализ.
Нелинейная регрессия позволяет подбирать к табличным данным нелинейное уравнение – параболу, гиперболу и др. Excel реализует нелинейность в виде экспоненты, т.е. подбирает кривую вида
y=b·mx (2)
которая позволяет наилучшим образом провести экспоненциальную
кривую по точкам данных, которые изменяются нелинейно.
Так, например, данные о росте населения почти всегда лучше описываются не прямой линией, а экспоненциальной кривой. При этом нужно помнить, что достоверное прогнозирование возможно только на участках подъёма или спуска кривой (при отрицательных значениях х), т.к. сама кривая (2) изменяется монотонно, без точек перегиба. Например, делать экспоненциальный прогноз для функции, изменяющейся синусоидально, можно только на участках подъёма или спуска функции, для чего её разбивают на соответствующие интервалы.
Множественная регрессия
Множественная регрессия представляет собой анализ более одного набора данных аргумента х и дает более реалистичные результаты. Множественный регрессионный анализ также может быть как линейным, так и экспоненциальным. Уравнения регрессии (1) и(2) примут соответственно вид (3) и (4):
у=mlxl + m2x2 +... + mnxn + b (3)
у = b·mlxl· m2x2 ·... · mnxn (4)
где:
xl, x2,..., xn - независимые переменные.
С помощью множественной регрессии, например, можно оценить стоимость дома в некотором районе, основываясь на данных его площади, размерах участка земли, этажности, вида из окон и т.д.
