ОПРЕДЕЛЕНИЕ КОНТАКТНЫХ НАПРЯЖЕНИЙ В ПРОЦЕССАХ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ
Цель работы – освоение метода фольговых датчиков для нахождения контактных напряжений; изучение распределения напряжений на поверхности открытого штампа; получение практических навыков обработки результатов эксперимента (4 часа).
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Метод фольговых датчиков
Условия работы деформирующего инструмента характеризуется интенсивным воздействием весьма высоких температурно-силовых нагрузок. Реактивные силы при деформировании заготовки вызывают упругую или упругопластическую деформацию отдельных участков инструмента являются причиной износа, появления трещин, а в отдельных случаях разрушения. Кроме того, от условий эксплуатации зависит теплопередача от заготовки к инструменту, условия контактного трения, особенности возникновения и развития разгарных трещин. Наконец, фазовые и структурные превращения в поверхностном слое инструмента происходят не только в связи с тепловым, но и силовым воздействием деформируемого металла на инструмент.
Развиваемые в процессе обработки металлов давлением контактные напряжения иногда превышают допустимые значения напряжений для металла инструмента. В результате этого имеет место смятие рабочих кромок матриц, пресс-шайб, образование глубоких трещин. Поэтому очень важно знать силовой режим деформирования и уровень контактных напряжений.
Одним из методов экспериментального определения нормальных контактных напряжений является метод фольговых датчиков, предложенный Я.М. Охрименко с сотрудниками.
На рис. 1 представлена схема измерения 111 с помощью фольговых датчиков. Для этого перпендикулярно поверхности инструмента просверливается отверстия малого диаметра 1 и закрываются фольгой 2 толщиной t из достаточно прочного и пластичного металла. После деформации металла на фольге остаются выпуклые отпечатки, по высоте которых h судят о величине нормальных напряжений на поверхности контакта. Обычно используется фольга толщиной t=0.1-0.3 мм.
Зафиксированное контактное давление: 
складывается из двух составляющих:
σк = σд + σз
где 
– действительное контактное давление на поверхности инструмента; 
– давление, зависящее от условия затекания металла в отверстие.
Для нахождения используют тарировочный график, связывающий величину с глубиной отпечатка h.
Тарировка датчиков производится полиуретаном в замкнутом объеме при различных значениях гидростатического давления σ (рис. 2). Шайба 1 с отверстиями 2 и с датчиком 3 устанавливаются в контейнере 4. При нажатии на пуансон 5 силой Р в закрытой полости контейнера с помощью полиуретана 6 создается гидростатическое давление. Нормальное напряжение σ, действующее на поверхность шайбы, определяется по выражению:
σ 
, а высота лунок h = 
где, Fк – площадь контактной поверхности, Fк = 
;
N – число отверстий на шайбе;
hi – высота лунки в i – ом отверстии;
D – диаметр контейнера для тарировки.
а) б)
Рис. 1. а) - схема измерений контактных напряжений с помощью фольговых датчиков; б) – тарировочный штамп.
1) Шайба с отверстиями; 2) Отверстия; 3) Датчик фольга; 4) Полиуретан; 5) Пуансон; 6) Контейнер.
Метод фольговых датчиков имеет недостатки:
· Не идентичность условий при образовании отпечатка на фольге в процессе тарировки и эксперимента;
· Фольговые датчики замеряют давление лишь в ограниченном количестве мест контактной поверхности. Измеренная величина давления является средней.
Аппроксимация экспериментальных данных
Методы аппроксимации осуществляют путём подбора, по возможности, простых аналитических формул, с достаточной степенью точности отображающих экспериментально полученные зависимости. Чаще всего вид общей формулы заранее неизвестен.
По характеру расположения экспериментальных точек на графике или анализа теоретической информации всегда можно установить примерный вид изучаемой зависимости.
Результаты экспериментов содержат случайные ошибки, поэтому нельзя требовать, чтобы подобранная формула точно соответствовала всем экспериментальным точкам Другими словами, график искомой функции не должен проходить через все точки. Желательно, чтобы отклонения результатов эксперимента, от значений, вычисленных по формуле, были как можно меньше.
Пусть в результате эксперимента получен ряд измерений, величин Уэ; У э1; Уэ2, …, Уэn соответствующих значениям аргумента X 1; X2, …, Xn, которые на графике представлены в виде точек Необходимо установить эмпирическую зависимость между X и Y. При этом принимают следующие допущения:
1) все значения переменной Хi являются точными, т.е. ошибками в их экспериментальном определении можно пренебречь
2) результаты эксперимента Уэ; У э1; Уэ2, …, Уэn являются независимыми случайными величинами, подчиняющимися нормальному закону распределения.
Уравнения, связывающие случайную величину У с неслучайной X, называются уравнениями регрессии по предложению Френсиса Гамильтона.
Пусть экспериментальная зависимость на рис. 2 аппроксимируется уравнением прямой вида Yi=axi, где a – постоянная, подлежащая определению.
Для нахождения a используют среднеарифметический метод и метод наименьших квадратов.
Рис. 2 Аппроксимация экспериментальных точек уравнения y = ax.
По методу средних или среднеарифметическому методу требуется, чтобы сумма разностей между значениями искомой величины, определенными по найденной формуле, и экспериментальными ее значениями равнялось нулю: 
Для уравнения y = ax имеем:
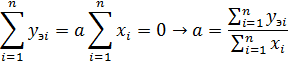
По методу наименьших квадратов (МНК), разработанному Гауссом более 170 лет назад, требуется, чтобы сумма квадратов разностей между значениями искомой величины, определенными по найденной формуле, и экспериментальными ее значениями была минимальной:
Для уравнения прямой вида yi = axi по методу наименьших квадратов
Для определения значения а надо взять производную по а от этой суммы и приравнять к нулю (n – число измерений):
