1. Задаем вектор х0 (начальное приближение), матрицу B = BT > 0.
2. Положим xk = x0, k = 0 (номер итерации)
3. Вычисляем вектор rk = Axk – b (невязка начального приближения).
4. Вычисляем вектор ωk = rkBk-1.
5. Вычисляем скаляр τk+1 = (Aωk, ωk) / (B-1Aωk, Aωk) (шаговый множитель).
6. Вычисляем вектор xk+1 = xk – τk+1 B-1Aωk (очередное приближение).
7. Вычисляем вектор rk+1 = Axk+1 – b. (невязка k+1 приближения).
8. Положим k = k + 1.
9. Проверяем выполнение неравенства ||rk||2 =< 0.001; если «да», то останавливаем работу алгоритма и выводим результаты, иначе возвращаемся к шагу 3.
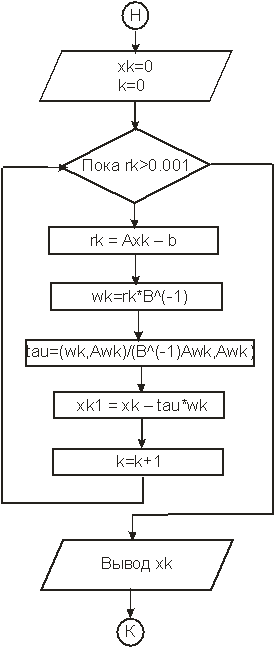
Рис.2 Блок-схема метода минимальных поправок
Метод скорейшего спуска
1. Задаем вектор х(0) (начальное приближение).
2. Положим xk = x0, k = 0 (номер итерации)
3. Вычисляем вектор rk = Axk – b (невязка начального приближения).
4. Вычисляем скаляр τk+1 = (rk, rk) / (Ark, Ark) (шаговый множитель).
5. Вычисляем вектор xk+1 = xk – τk+1rk (очередное приближение).
6. Вычисляем вектор rk+1 = Axk+1 – b. (невязка k+1 приближения).
7. Положим k = k + 1.
8. Проверяем выполнение неравенства ||rk||2 =< 0.001; если «да», то останавливаем работу алгоритма и выводим результаты, иначе возвращаемся к шагу 3.

Рис.3 Блок-схема метода скорейшего спуска
Метод сопряженных градиентов
1. Задаем вектор х(0) (начальное приближение).
2. Положим xk = x0, k = 0 (номер итерации)
3. Вычисляем вектор rk = Axk – b (невязка начального приближения).
4. Положим вектор pk= rk (сопряженный вектор)
5. Вычисляем скаляр αk = (rk, rk) / (Apk, pk).
6. Вычисляем вектор xk+1 = xk + αk pk (очередное приближение)
7. Вычисляем вектор rk+1 = rk - αk Apk. (невязка k+1 приближения)
8. Вычисляем скаляр βk = (rk+1, rk+1) / (rk, rk).
9. Проверяем выполнение неравенства ||rk+1||2 =< 0.001; если «да», то останавливаем работу алгоритма и выводим результаты
10.. Вычисляем pk+1= rk+1+ βkpk
11. Положим k = k + 1.
12. Возвращаемся к шагу 5
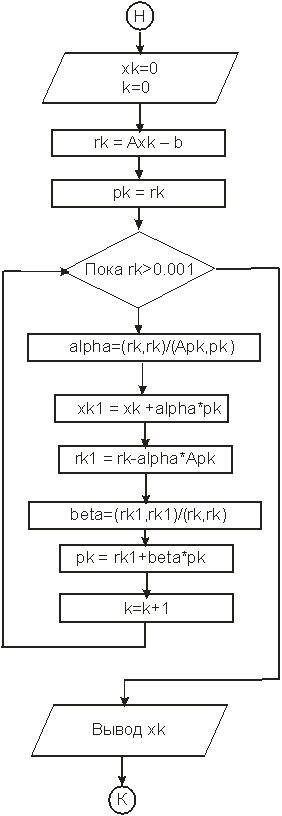
Рис.4 Блок-схема метода сопряжённых градиентов
Руководство пользователя.
В окне программы пользователю предлагается ввести размерность матрицы системы и требуемую точность, также при желании можно задать величину диагонального преобладания, либо убрать преобладание вообще (см. рис.5)

Рис.5 Окно программы
При нажатии на кнопку ОК генерируется симметричная матрица заданной размерности, а также правая часть. Далее, при нажатии на кнопку с названием метода, в соответствующий столбец выводится решение и количество итераций (см. рис. 6).

Рис.6 Решение системы с матрицей размерностью 10х10
Матрицу можно модифицировать, прибавив к главной диагонали заданную величину, для этого нужно ввести необходимую величину в поле «Преобладание», поставить флаг «Модифицировать» и нажать ОК.
Также существует возможность записи сгенерированной матрицы в файл и чтения существующей матрицы из файла. Пользователь может выбрать для записи и чтения один из трёх файлов.






